Vous connaissez cet adage, « on ne voit pas la forêt pour les arbres »? Eh bien, les chercheurs en sciences sociales sont confrontés à un problème similaire lorsqu’ils analysent des données. Ils disposent de beaucoup d’informations à portée de main, mais il est souvent difficile de discerner les modèles et les relations cachés au sein de tous ces chiffres.
C’est là qu’intervient l’analyse factorielle exploratoire (AFE), une technique statistique qui aide les chercheurs à donner un sens à leurs données en identifiant les facteurs sous-jacents qui expliquent les corrélations entre les variables. Dans cet article, nous expliquerons ce qu’est l’AFE, pourquoi elle est utile et comment la mener étape par étape.
Que vous soyez un étudiant diplômé se lançant dans votre premier projet de recherche ou un professionnel expérimenté cherchant à élargir votre boîte à outils quantitatifs, ce guide pour débutants vous donnera une base solide en AFE. Nous aborderons tout, des hypothèses sous-jacentes à cette technique aux exemples concrets montrant comment la méthode peut éclairer des ensembles de données complexes.
Alors installez-vous confortablement et préparez-vous à découvrir comment l’analyse factorielle exploratoire peut vous aider à voir au-delà des points de données individuels et à découvrir des modèles plus larges qui se cachent en dessous de la surface.
Comprendre l’analyse factorielle exploratoire
Au cœur de l’analyse factorielle exploratoire, les chercheurs identifient les facteurs sous-jacents qui expliquent pourquoi certaines variables sont corrélées les unes avec les autres.
Vous vous demandez peut-être comment l’EFA diffère d’une autre technique appelée analyse factorielle commune. La principale distinction réside dans leurs objectifs : tandis que l’AFC vise à confirmer des hypothèses préexistantes sur la manière dont les variables sont liées les unes aux autres, l’EFA vise à découvrir des modèles sous-jacents qui n’ont peut-être pas été considérés auparavant.
Alors, comment fonctionne exactement l’EFA ? Disons que nous examinons un ensemble de données sur les traits de personnalité. Nous pourrions commencer par identifier un ensemble de variables (par exemple, extraversion, amabilité, conscienciosité) et exécuter une EFA pour voir s’il existe des facteurs sous-jacents qui influencent ces traits. À partir de là, nous pouvons calculer des scores de facteur pour chaque participant en fonction de ses réponses à ces variables.
Bien sûr, il n’est pas toujours facile de déterminer quels facteurs sont les plus importants – c’est là que des éléments tels que la détermination du nombre approprié de facteurs ou l’interprétation des charges factorielles entrent en jeu. Mais l’idée de base derrière l’EFA est simple : en identifiant les facteurs latents qui sous-tendent les variables observables, nous pouvons obtenir des insights plus profonds dans des ensembles de données complexes.
Pensez-y de cette façon : tout comme un arbre a des racines sous la surface qui soutiennent sa croissance au-dessus du sol, les ensembles de données ont également des structures sous-jacentes qui façonnent leur apparence à la surface. En utilisant des techniques d’analyse factorielle exploratoire telles que la dérivation des valeurs propres ou la réalisation d’analyses parallèles (plus sur celles-ci plus tard !), les chercheurs peuvent commencer à déterrer ces racines cachées et comprendre ce qui se cache en dessous.
En bref, l’analyse factorielle exploratoire offre aux chercheurs un outil incroyablement puissant pour étudier des ensembles de données complexes et comprendre comment différents aspects de ces ensembles de données interagissent les uns avec les autres au fil du temps. Que vous travailliez avec des traits de personnalité, des prix d’actions ou tout ce qui se trouve entre les deux, maîtriser cette technique vous aidera à débloquer de nouvelles perspectives sur vos données.
Le but de l’analyse factorielle exploratoire
Lorsqu’il s’agit d’analyser des ensembles de données complexes, l’un des outils les plus puissants à la disposition d’un chercheur est l’analyse factorielle exploratoire. Mais quelle est exactement la raison d’être de cette technique ? En bref, l’EFA nous aide à comprendre comment différentes variables de notre ensemble de données sont liées les unes aux autres en identifiant les facteurs latents qui les sous-tendent.
Pour ce faire, l’EFA s’appuie sur des techniques telles que l’analyse en composantes principales et la rotation factorielle, qui permettent aux chercheurs d’identifier des motifs dans les corrélations entre les variables. En examinant ces motifs et en calculant des choses comme les valeurs propres et les charges factorielles, nous pouvons commencer à reconstituer une compréhension plus complète de la façon dont fonctionnent nos données.
Un avantage clé de l’EFA par rapport à d’autres techniques telles que l’analyse en composantes principales est qu’elle prend en compte les corrélations entre les variables plutôt que de simplement examiner leur variance globale. Cela signifie que si deux variables sont fortement corrélées entre elles mais pas avec d’autres dans l’ensemble de données, elles seront regroupées ensemble en tant que partie d’un facteur sous-jacent unique – quelque chose que l’ACP manquerait complètement.
Bien sûr, mener une EFA n’est pas toujours simple – il y a de nombreuses décisions à prendre en cours de route concernant des choses comme la matrice de corrélation à utiliser ou le nombre de facteurs à extraire de vos données. Mais en examinant attentivement ces choix et en interprétant vos résultats à travers une lentille de variance totale expliquée ou de statistiques de qualité d’ajustement (comme la mesure de Kaiser-Meyer-Olkin), vous pouvez obtenir des informations précieuses même sur les ensembles de données les plus complexes.
Alors pourquoi choisir l’analyse factorielle exploratoire plutôt qu’une autre technique telle que l’analyse factorielle confirmatoire ? Bien que l’AFC offre plus de contrôle sur la spécification du modèle et les tests d’hypothèses, elle nécessite également une connaissance préalable solide de la façon dont vos variables sont liées les unes aux autres – quelque chose qui peut ne pas toujours être disponible ou fiable. Avec les techniques d’analyse factorielle exploratoire à votre disposition, vous êtes libre d’explorer de nouvelles façons de penser à vos données sans être contraint par des idées préconçues ou des hypothèses.
En bref : que vous travailliez sur des projets de recherche en sciences sociales ou que vous analysiez des données marketing à des fins commerciales (ou tout autre chose !), l’analyse factorielle exploratoire offre un ensemble d’outils incroyablement polyvalent pour découvrir les structures cachées au sein de grands ensembles de données. Alors n’hésitez pas à plonger et à commencer à explorer !
Avant de procéder à une analyse factorielle exploratoire, définissez clairement la question de recherche ou le problème que vous essayez de résoudre. Cela aidera à guider votre analyse et à vous assurer que vous utilisez des méthodes et des techniques appropriées. De plus, soyez ouvert d’esprit et disposé à explorer différentes solutions – l’analyse factorielle peut révéler des relations et des idées inattendues qui peuvent conduire à de nouvelles avenues de recherche.
Assumptions of Exploratory Factor Analysis
Pour mener une analyse factorielle exploratoire efficace, il y a plusieurs hypothèses clés que les chercheurs doivent prendre en compte. Celles-ci incluent des choses comme les correlations entre les facteurs dans notre ensemble de données et l’idée de factors communs ou de variables sous-jacentes qui entraînent ces corrélations.
Une hypothèse importante est que nos variables devraient être au moins modérément corrélées les unes avec les autres afin de pouvoir identifier des facteurs sous-jacents significatifs. C’est là que des techniques comme l’analyse en composantes principales sont utiles – en réduisant le nombre de variables avec lesquelles nous travaillons, nous pouvons plus facilement découvrir des structures d’ordre supérieur au sein de nos données.
Une autre hypothèse clé implique de comprendre la distinction entre les factors corrélés et les vrais facteurs sous-jacents. Les facteurs corrélés peuvent sembler avoir une forte relation en surface, mais cela pourrait simplement être dû à une variance partagée plutôt qu’à une connexion plus profonde entre eux. En utilisant des techniques de rotation factorielle (comme varimax ou oblique), les chercheurs peuvent aider à démêler ces relations et obtenir une image plus claire de ce qui conduit vraiment leurs données.
En même temps, il est important de ne pas négliger d’autres sources potentielles de variation au sein de notre ensemble de données – par exemple, l’erreur de mesure ou la variance unique spécifique à certains éléments ou questions. En considérant soigneusement tous ces éléments différents ensemble lors de la réalisation d’une EFA, nous pouvons nous assurer que nos résultats sont robustes et fiables.
En fin de compte, bien qu’il y ait de nombreuses hypothèses impliquées dans l’analyse factorielle exploratoire (et en effet toute technique statistique), son pouvoir réside dans sa capacité à nous aider à découvrir de nouveaux modèles et idées au sein de jeux de données complexes – même ceux où nous ne nous y attendions pas initialement ! Donc, si vous cherchez un ensemble d’outils qui vous permet une plus grande flexibilité et créativité lorsque vous explorez vos données, l’EFA pourrait bien être exactement ce dont vous avez besoin !
Avant de réaliser une analyse factorielle exploratoire, il est important de prendre en compte attentivement les hypothèses de la méthode. Celles-ci incluent des facteurs tels que la taille de l’échantillon, la structure de corrélation et la distribution des variables. En comprenant ces hypothèses et en veillant à ce qu’elles soient respectées, vous pouvez augmenter l’exactitude et la fiabilité de vos résultats.
Étapes impliquées dans la réalisation d’une analyse factorielle exploratoire
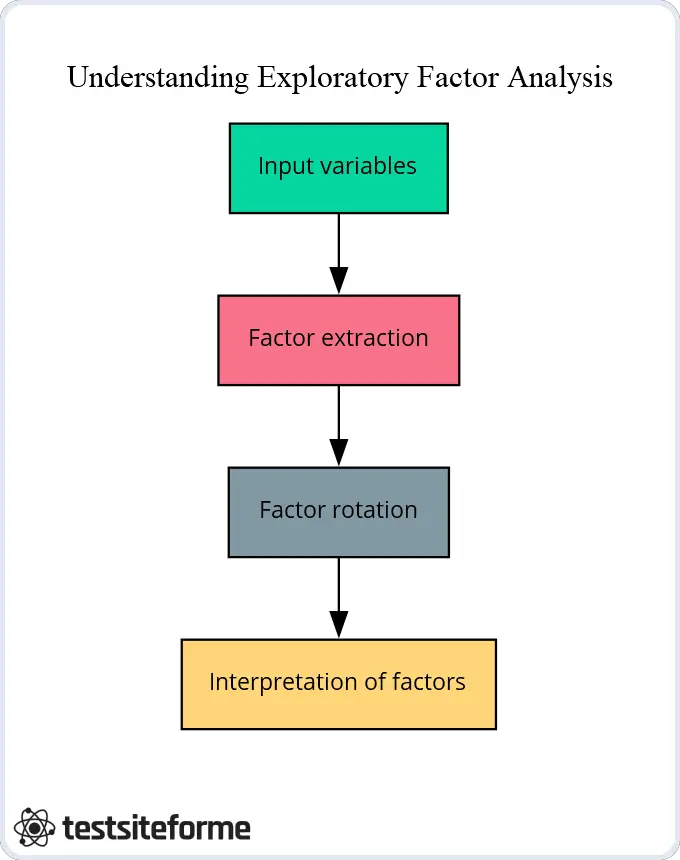
Lorsqu’il s’agit de mener une analyse factorielle exploratoire, il y a plusieurs étapes clés que les chercheurs doivent suivre afin d’obtenir le meilleur résultat possible à partir de leurs données. Celles-ci comprennent la sélection de méthodes d’extraction appropriées pour identifier les facteurs sous-jacents et l’application de rotations de facteurs pour aider à clarifier la structure factorielle.
Voici quelques-unes des étapes clés impliquées dans la réalisation d’une EFA réussie :
- Choisissez votre méthode d’extraction : Il existe plusieurs techniques différentes disponibles pour extraire les facteurs de votre ensemble de données, chacune ayant ses propres forces et faiblesses. Certaines options courantes comprennent la facturation de l’axe principal, l’estimation du maximum de vraisemblance ou l’extraction des résidus minimums (OLS). Selon vos questions de recherche spécifiques et vos besoins, vous voudrez peut-être expérimenter différentes méthodes jusqu’à ce que vous trouviez celle qui fonctionne le mieux pour vous.
- Déterminez le nombre de facteurs à extraire : Une fois que vous avez choisi une méthode d’extraction, il est temps de décider combien de facteurs vous voulez extraire de votre ensemble de données – cela dépendra de divers facteurs tels que la taille de l’échantillon et la complexité des variables considérées.
- Appliquer une rotation de facteurs : Afin de mieux comprendre les relations entre nos facteurs extraits (et éviter le surajustement), nous appliquons souvent des techniques de rotation de facteurs telles que la rotation varimax ou oblique qui peuvent nous aider à identifier des motifs plus significatifs dans nos données en réduisant le bruit et en augmentant la clarté.
- Interpréter les résultats : Enfin, une fois que nous avons terminé toutes ces étapes, nous pouvons commencer à interpréter nos résultats en examinant des éléments tels que les chargements factoriels, les valeurs propres, les graphiques en éboulis, etc., qui peuvent nous donner un aperçu des structures sous-jacentes qui pourraient être à l’origine de nos données.
Comme l’a dit le célèbre inventeur Thomas Edison : « Le génie est fait de 1 % d’inspiration et de 99 % de transpiration » – c’est aussi le cas lorsqu’on utilise l’analyse factorielle exploratoire !
Étapes de la réalisation d’une EFA
Le tableau ci-dessous résume les étapes impliquées dans la réalisation d’une EFA, y compris l’extraction des facteurs, la rotation et l’interprétation. Utilisez-le comme guide de référence lors de la réalisation de votre propre EFA.
| Étape | Description |
|---|---|
| Extraction des facteurs | Identifier le nombre de facteurs à extraire et effectuer une analyse factorielle préliminaire. |
| Rotation des facteurs | Faire tourner les facteurs extraits pour simplifier la structure factorielle et augmenter l’interprétabilité. |
| Interprétation des facteurs | Interpréter la structure factorielle finale en examinant les chargements factoriels et en identifiant des noms de facteurs significatifs. |
Taille de l’échantillon et adéquation de l’échantillonnage pour l’EFA
Lorsqu’il s’agit de mener une analyse factorielle exploratoire, l’une des considérations les plus importantes est la taille de l’échantillon et l’adéquation de l’échantillonnage. Cela est dû au fait que si notre taille d’échantillon est trop petite, nous pourrions ne pas avoir suffisamment de puissance statistique pour détecter des relations significatives entre les variables dans nos données.
De même, si notre erreur de mesure ou variance d’erreur est élevée (par exemple, en raison de mesures brutes de mauvaise qualité), cela peut également réduire l’exactitude de nos résultats et rendre plus difficile l’identification des facteurs sous-jacents. Par conséquent, lors de la réalisation de l’EFA, il est important que nous examinions attentivement à la fois la quantité et la qualité des données utilisées.
Heureusement, il existe plusieurs façons de tester l’adéquation de l’échantillonnage avant de procéder à l’EFA. Une technique populaire consiste à calculer une statistique appelée Kaiser-Meyer-Olkin (KMO), qui mesure la pertinence de vos données pour l’analyse factorielle en examinant les corrélations entre les variables dans votre ensemble de données.
En règle générale, les valeurs de KMO supérieures à 0,6 sont considérées comme adéquates pour l’EFA, bien que certains chercheurs préfèrent des seuils plus élevés en fonction de leurs questions ou objectifs de recherche. En plus des valeurs de KMO, vous voudrez peut-être également inspecter d’autres mesures diagnostiques telles que le test de sphéricité de Bartlett, qui teste si les intercorrelations entre les variables sont suffisamment différentes de zéro pour ne pas être redondantes les unes avec les autres.
Bien que la taille de l’échantillon et l’adéquation de l’échantillonnage puissent sembler être des détails techniques au premier abord, ce sont en fait des facteurs incroyablement importants qui peuvent avoir un impact sur la validité et la fiabilité des résultats de votre étude ! Vous serez mieux équipé que jamais pour découvrir des modèles cachés même dans des ensembles de données complexes sans vous soucier des problèmes liés à l’erreur de mesure ou à des tailles d’échantillon inadéquates qui pourraient entraver votre progression.
Lors de la réalisation d’une analyse factorielle exploratoire, il est essentiel de veiller à ce que la taille de votre échantillon soit adéquate et que votre méthode d’échantillonnage soit appropriée pour la question de recherche en cours. Tenez compte de facteurs tels que la complexité des données et le nombre de variables analysées pour déterminer une taille d’échantillon appropriée, et assurez-vous d’utiliser un échantillon représentatif qui reflète avec précision la population que vous étudiez.
Détermination du nombre de facteurs dans l’analyse factorielle exploratoire
Lors de la réalisation d’une analyse factorielle exploratoire, l’une des étapes les plus critiques est la détermination du nombre de facteurs à extraire à partir de vos données. Cela peut être difficile car vous pouvez avoir plusieurs facteurs – à la fois actifs et inactifs – qui composent vos variables mesurées.
Une approche souvent utilisée par les chercheurs est l’examen d’un graphique en épi, qui montre combien de facteurs sont nécessaires pour expliquer des portions de plus en plus grandes de la variance dans l’ensemble de données. En général, nous cherchons un point de courbure ou de « coude » où l’ajout de facteurs supplémentaires ne fournit plus de gains substantiels en termes de pouvoir explicatif.
Une autre technique qui peut être utile est l’inspection des valeurs propres associées à chaque facteur. Essentiellement, ces valeurs représentent la quantité de variation dans nos données qui peut être expliquée par chaque facteur individuel – les valeurs plus élevées indiquant des dimensions ou des modèles plus importants au sein de notre ensemble de données.
Bien sûr, il convient de noter qu’il n’y a pas toujours une réponse claire lorsqu’il s’agit de décider du nombre optimal de facteurs pour l’analyse factorielle exploratoire. Selon vos questions de recherche et vos objectifs, il peut être approprié d’extraire plus (ou moins) de dimensions ! Cependant, ce qui est important, c’est que vous considériez attentivement toutes les preuves disponibles avant de parvenir à des conclusions finales sur le nombre de composantes sous-jacentes présentes dans vos données.
En fin de compte, l’utilisation de techniques telles que les graphiques en épi et l’inspection des valeurs propres peut nous aider à déterminer si nous avons besoin d’extraire 2-3 facteurs larges ou des dizaines de facteurs étroits – réduisant la subjectivité et assurant la cohérence entre différents ensembles de données !
En pratique, la détermination du nombre approprié de facteurs dans l’analyse factorielle exploratoire nécessite une réflexion attentive ainsi que de l’intuition statistique sur les dimensions les plus importantes dans votre contexte d’étude particulier. En pesant plusieurs éléments de preuve ensemble (comme les graphiques en épi et les valeurs propres), vous serez bien équipé pour identifier des modèles significatifs même dans des ensembles de données complexes sans vous perdre dans les détails inutiles.
Méthodes pour déterminer le nombre de facteurs dans l’analyse factorielle exploratoire
Ce tableau montre les méthodes couramment utilisées pour déterminer le nombre de facteurs dans l’analyse factorielle exploratoire, y compris la règle de Kaiser, le graphique en épi et l’analyse parallèle.
| Méthode | Description |
|---|---|
| Règle de Kaiser | Conserver tous les facteurs avec des valeurs propres supérieures à 1 |
| Graphique en épi | Tracer les valeurs propres en fonction du numéro du facteur et conserver les facteurs avant le point de « coude » |
| Analyse parallèle | Générer des ensembles de données aléatoires et comparer les valeurs propres aux valeurs propres réelles des données pour déterminer le nombre de facteurs à conserver |
Interprétation des résultats d’EFA : Charges factorielles et valeurs propres
Alors que nous continuons à explorer l’analyse factorielle exploratoire, il est essentiel de comprendre comment interpréter les résultats obtenus grâce à cette technique. Deux des composantes les plus critiques qui nécessitent une attention particulière comprennent les charges factorielles et les valeurs propres.
Tout d’abord, les charges factorielles sont essentiellement des coefficients qui représentent la contribution de chaque variable mesurée à une variable latente ou dimension donnée. En d’autres termes, elles nous indiquent quelles variables sont le plus fortement associées à des facteurs spécifiques dans nos données, nous permettant ainsi d’identifier des modèles sous-jacents et des relations qui pourraient ne pas être immédiatement apparents à première vue.
De plus, ces coefficients peuvent nous aider à comprendre comment différentes dimensions sont liées les unes aux autres, offrant ainsi une compréhension plus nuancée de nos données au-delà de ce que les simples corrélations peuvent offrir.
Deuxièmement, les valeurs propres jouent également un rôle crucial dans l’interprétation de l’EFA. Ces valeurs indiquent la quantité de variation expliquée par chaque variable latente ou facteur par rapport à tous les autres inclus dans l’analyse.
Il est important de noter cependant que, comme l’EFA produit généralement plusieurs valeurs propres (une pour chaque variable latente), il est nécessaire d’utiliser une méthode de rotation (par exemple, varimax) lors de l’interprétation de ces résultats.
Ce processus aide à garantir que nous ne prenons en compte que des sources uniques de variance à travers différentes dimensions plutôt que de simplement reproduire des informations déjà capturées par des facteurs antérieurs.
Dans l’ensemble, l’interprétation des résultats d’EFA nécessite une considération attentive à la fois des charges factorielles et des valeurs propres, ainsi qu’une compréhension des différentes techniques statistiques telles que les méthodes de rotation. En examinant ces sorties en conjonction avec vos questions de recherche et vos objectifs en tête, vous serez en mesure d’obtenir des informations approfondies sur des ensembles de données complexes sans vous encombrer de détails inutiles !
Exemples concrets d’analyse factorielle exploratoire
Les applications réelles de l’analyse factorielle exploratoire sont nombreuses dans des domaines tels que la psychologie, la sociologie et la recherche en marketing. Ces applications visent à identifier les facteurs potentiels qui sous-tendent des ensembles de données complexes et à fournir une compréhension plus nuancée des relations entre différentes variables.
Par exemple, dans une étude visant à identifier les prédicteurs de la satisfaction au travail parmi les travailleurs de la santé, l’EFA a été utilisée pour analyser les réponses de plusieurs questionnaires. L’analyse statistique a révélé quatre facteurs distincts qui étaient le plus fortement associés à la satisfaction globale au travail : le soutien du superviseur, la culture organisationnelle, le contrôle de la charge de travail et l’autonomisation du personnel.
De plus, les coefficients de corrélation obtenus par l’EFA ont montré que ces facteurs étaient fortement interdépendants, ce qui indique l’importance de prendre en compte plusieurs dimensions lors de l’examen du bien-être des employés dans ce contexte.
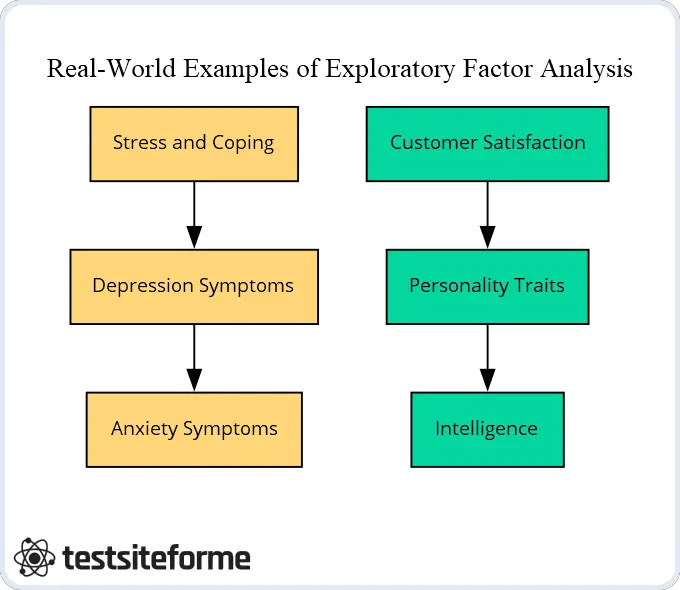
Dans un autre exemple d’études de simulation impliquant des ensembles de données à grande échelle collectées lors d’essais cliniques pour des médicaments de traitement de la dépression, les chercheurs ont utilisé l’EFA pour identifier les variables latentes sous-jacentes à différents aspects de la symptomatologie de la dépression tels que la tristesse ou l’anédonie (l’incapacité à éprouver du plaisir). Ils ont trouvé des preuves soutenant l’existence d’un seul facteur représentant les symptômes de détresse générale plutôt que plusieurs distincts liés uniquement à des types spécifiques d’affectivité négative (par exemple, l’anxiété).
Ces résultats soulignent comment l’EFA peut aider à découvrir des schémas précédemment inconnus au sein d’ensembles de données complexes, conduisant finalement les chercheurs vers des conclusions mieux informées sur leurs objectifs de recherche.
Avantages et Limitations de l’Analyse Factorielle Exploratoire
L’analyse factorielle exploratoire présente plusieurs avantages qui en font une technique populaire pour l’analyse de jeux de données complexes. Par exemple, l’AFE permet aux chercheurs d’identifier les facteurs psychologiques sous-jacents à plusieurs variables observées – offrant une compréhension plus holistique de la manière dont les différents aspects du concept sont liés les uns aux autres.
De plus, l’AFE peut aider à découvrir des facteurs uniques et des variances idiosyncratiques qui pourraient être manqués en utilisant des méthodes statistiques traditionnelles. En explorant ces dimensions uniques, les chercheurs peuvent obtenir de nouvelles perspectives sur des phénomènes complexes tels que les traits de personnalité ou les styles d’apprentissage.
Cependant, il existe également des limites associées à l’AFE. Un problème potentiel est de déterminer le nombre approprié de facteurs dans l’analyse – ce qui peut être difficile s’il y a de nombreuses variables fortement corrélées et aucun cadre théorique clair pour guider la sélection.
De plus, l’AFE suppose que les variables observées ont une relation linéaire avec les constructions latentes sous-jacentes – ce qui peut ne pas toujours être vrai dans les jeux de données du monde réel. Enfin, l’estimation du maximum de vraisemblance utilisée dans les modèles d’analyse factorielle exploratoire nécessite des échantillons importants pour obtenir des résultats précis; sinon, de petits échantillons peuvent entraîner des chargements de facteurs instables ou des conclusions peu fiables.
Malgré ces limites, l’analyse factorielle exploratoire reste un outil essentiel pour découvrir des relations entre différentes variables mesurées et pour découvrir des structures cachées dans les ensembles de données. Qu’il soit appliqué dans le contexte des sciences sociales ou de la recherche de marché, il offre aux analystes des perspectives puissantes sur les tendances et les modèles qu’ils n’auraient peut-être pas été en mesure de discerner autrement.
En fin de compte, bien que l’analyse factorielle exploratoire ne soit pas parfaite, ses avantages l’emportent largement sur ses inconvénients lorsqu’elle est appliquée de manière appropriée par des praticiens informés qui comprennent à la fois ses forces et ses faiblesses.
Comparaison de l’EFA avec l’analyse factorielle confirmatoire
En ce qui concerne l’analyse factorielle, l’analyse factorielle confirmatoire (CFA) est souvent comparée à l’analyse factorielle exploratoire. Bien que les deux méthodes visent à identifier les facteurs latents qui sous-tendent les variables observées, il existe plusieurs différences entre les deux approches.
Tout d’abord, la CFA teste un modèle prédéterminé de la relation entre les variables observées et les facteurs sous-jacents, tandis que l’EFA permet aux chercheurs d’explorer comment différentes variables pourraient être liées sans aucune hypothèse spécifique sur la corrélation. Cela signifie qu’avec la CFA, les analystes doivent avoir un cadre théorique clair en tête avant de procéder à leurs analyses, tandis que l’EFA peut aider à générer des hypothèses et des théories pour des tests ultérieurs.
Deuxièmement, les CFA supposent une corrélation nulle entre les facteurs sauf si elle est explicitement spécifiée dans le modèle, tandis que les EFA permettent à toutes les paires de facteurs de covarier par défaut. Un avantage de cette hypothèse est qu’elle contribue à minimiser les problèmes de multicollinéarité associés aux constructions latentes fortement corrélées.
Troisièmement, alors que l’analyse factorielle exploratoire utilise des corrélations polychoriques comme données d’entrée lorsqu’elle travaille avec des types de données catégorielles ou ordinales, la CFA applique des corrélations partielles uniquement sur les phénotypes continus.
Malgré ces différences d’approche et de méthodologie, les deux techniques sont des méthodes psychologiques précieuses pour découvrir les relations entre les constructions cachées dans les ensembles de données. Cependant, le choix de la méthode qui fonctionne le mieux dépend des questions de recherche spécifiques posées et du type de données avec lesquelles vous travaillez : catégorielles vs continues ou axées sur la théorie vs génératrices d’hypothèses.
Pour réitérer, l’analyse factorielle exploratoire permet aux chercheurs d’explorer des modèles complexes sans hypothèses a priori, tandis que les analyses factorielles confirmatoires nécessitent des modèles prédéterminés mais permettent des tests d’hypothèses plus précis compte tenu de leur formulation explicite. Les deux méthodes ont leurs propres forces et faiblesses selon le type de problème que vous essayez de résoudre !
Conclusion : Quand utiliser l’analyse factorielle exploratoire dans les projets de recherche
En recherche en sciences sociales, l’ analyse factorielle exploratoire (AFE) est un outil utile pour identifier les facteurs sous-jacents qui entraînent la variance commune parmi les variables observées. L’AFE aide les chercheurs à explorer les relations entre différentes variables et à analyser comment elles pourraient être liées dans des combinaisons linéaires.
L’un des principaux avantages de l’AFE est sa capacité à identifier des constructions latentes – telles que des traits de personnalité ou des attitudes – qui ne sont pas directement observables mais qui peuvent avoir des impacts significatifs sur le comportement. En utilisant l’AFE, les chercheurs peuvent découvrir ces facteurs cachés et mieux comprendre leur rôle dans la formation de différents résultats.
Un autre avantage de l’AFE est sa flexibilité dans la manipulation de divers types de données – qu’elles soient continues ou catégorielles. Par exemple, lorsqu’on travaille avec des données catégorielles comme les réponses à des enquêtes sur une échelle de 1 à 5, des techniques de variables fictives peuvent être utilisées pour les transformer en valeurs numériques significatives pour une analyse ultérieure.
Cependant, il est important de noter que bien que l’analyse factorielle exploratoire puisse révéler des informations précieuses sur des ensembles de données complexes, elle ne doit être utilisée que comme outil exploratoire et non comme méthode unique pour tester des hypothèses ou valider des modèles en raison de son manque d’assomptions de cadre théorique prédéterminées comme le CFA.
Alors, quand devriez-vous utiliser l’analyse factorielle exploratoire ? Si vous voulez découvrir des modèles parmi vos variables observées sans aucune idée préconçue sur leurs relations ou si vous avez besoin de preuves préliminaires avant de passer à des méthodes plus rigoureuses, essayez l’analyse factorielle exploratoire ! N’oubliez simplement pas que bien qu’elle soit excellente pour générer des hypothèses, les analyses factorielles confirmatoires nécessitent des modèles prédéterminés qui permettent des tests d’hypothèses plus précis avec une formulation explicite.







