You know that old saying, “you can’t see the forest for the trees”? Well, social science researchers face a similar problem when analyzing data. They’ve got a lot of information at their fingertips, but it’s often tough to discern patterns and relationships hidden within all those numbers.
Enter exploratory factor analysis (EFA), a statistical technique that helps researchers make sense of their data by identifying underlying factors that explain the correlations between variables. In this article, we’ll break down what EFA is, why it’s useful, and how to conduct it step-by-step.
Whether you’re a graduate student embarking on your first research project or an experienced professional looking to expand your quantitative toolkit, this beginner’s guide will give you a solid grounding in EFA. We’ll cover everything from the assumptions that underlie this technique to real-world examples showing how the method can shed light on complex datasets.
So settle in and get ready to discover how exploratory factor analysis can help you see beyond individual data points and uncover broader patterns lurking beneath the surface.
Understanding Exploratory Factor Analysis
At its core, exploratory factor analysis helps researchers identify the underlying factors that explain why certain variables are correlated with each other.
Now, you might be wondering how EFA is different from another technique called common factor analysis. The main distinction lies in their purposes: while CFA aims to confirm pre-existing hypotheses about how variables relate to each other, EFA aims to uncover underlying patterns that may not have been considered before.
So how exactly does EFA work? Let’s say we’re looking at a dataset on personality traits. We might start by identifying a set of variables (e.g., extraversion, agreeableness, conscientiousness) and running an EFA to see if there are any underlying factors that influence these traits. From there, we can calculate factor scores for each participant based on their responses to these variables.
Of course, it’s not always straightforward figuring out which factors are most important – that’s where things like determining the appropriate number of factors or interpreting factor loadings come into play. But the basic idea behind EFA is simple: by identifying latent factors that underlie observable variables, we can gain deeper insights into complex datasets.
Think of it this way: just as a tree has roots beneath the surface that support its growth above ground, so too do datasets have underlying structures that shape their appearance on the surface. By using exploratory factor analysis techniques like deriving eigenvalues or conducting parallel analyses (more on those later!), researchers can begin to unearth those hidden roots and understand what lies beneath them.
In short, exploratory factor analysis offers researchers an incredibly powerful tool for investigating complex datasets and understanding how various aspects of those datasets interact with one another over time. Whether you’re working with personality traits or stock prices or anything in between, mastering this technique will help you unlock new insights into your data.
The Purpose of Exploratory Factor Analysis
When it comes to analyzing complex datasets, one of the most powerful tools at a researcher’s disposal is exploratory factor analysis. But what exactly is the purpose of this technique? Put simply, EFA helps us understand how different variables in our dataset relate to each other by identifying latent factors that underlie them.
To do so, EFA relies on techniques like principal component analysis and factor analytic rotation, which allow researchers to identify patterns in the correlations between variables. By examining these patterns and calculating things like eigenvalues and factor loadings, we can begin to piece together a more comprehensive understanding of how our data works.
One key advantage of EFA over other techniques like principal component analysis is that it takes into account correlations between variables rather than just looking at their overall variance. This means that if two variables are highly correlated with each other but not with any others in the dataset, they will be grouped together as part of a single underlying factor – something that PCA would miss entirely.
Of course, conducting an EFA isn’t always straightforward – there are many decisions to be made along the way about things like which correlation matrix to use or how many factors should be extracted from your data. But by carefully considering these choices and interpreting your results through a lens of total variance explained or goodness-of-fit statistics (such as Kaiser-Meyer-Olkin measure), you can gain valuable insights into even the most complex datasets.
So why might you choose exploratory factor analysis over another technique like confirmatory factor analysis? While CFA offers more control over model specification and hypothesis testing, it also requires strong prior knowledge about how your variables relate to each other – something that may not always be available or reliable. With exploratory factor analysis techniques at your disposal though, you’re free to explore new ways of thinking about your data without being constrained by preconceived notions or assumptions.
In short: whether you’re working on social science research projects or analyzing marketing data for business purposes (or anything else!), exploratory factor analysis provides an incredibly versatile toolset for uncovering hidden structures within large datasets. So don’t hesitate to dive in and start exploring!
Before conducting exploratory factor analysis, clearly define the research question or problem you are trying to solve. This will help guide your analysis and ensure that you are using appropriate methods and techniques. Additionally, be open-minded and willing to explore different solutions – factor analysis can reveal unexpected relationships and insights that can lead to new avenues of research.
Assumptions of Exploratory Factor Analysis
To conduct an effective exploratory factor analysis, there are several key assumptions that researchers must take into account. These include things like the correlations among factors in our dataset and the idea of common factors or underlying variables that drive those correlations.
One important assumption is that our variables should be at least moderately correlated with each other in order to make it possible to identify meaningful underlying factors. This is where techniques like principal components analysis come in handy – by reducing the number of variables we’re working with, we can more easily uncover higher-order structures within our data.
Another key assumption involves understanding the distinction between correlated factors and true underlying factors. Correlated factors may appear to have a strong relationship on the surface, but this could simply be due to shared variance rather than any deeper connection between them. By using techniques like factor analytic rotation (such as varimax or oblique), researchers can help disentangle these relationships and get a clearer picture of what’s really driving their data.
At the same time, it’s important not to overlook other potential sources of variation within our dataset – for example, measurement error or unique variance specific to certain items or questions. By carefully considering all these different elements together when conducting an EFA, we can ensure that our results are robust and reliable.
Ultimately though, while there are many assumptions involved in exploratory factor analysis (and indeed any statistical technique), its power lies in its ability to help us uncover new patterns and insights within complex datasets – even ones where we might not have expected them initially! So if you’re looking for a toolset that allows you greater flexibility and creativity when exploring your data, EFA might just be exactly what you need!
Before conducting exploratory factor analysis, it’s important to carefully consider the assumptions of the method. These include factors such as sample size, correlation structure, and variable distribution. By understanding these assumptions and ensuring that they are met, you can increase the accuracy and reliability of your results.
Steps Involved in Conducting an Exploratory Factor Analysis
When it comes to conducting an exploratory factor analysis, there are several key steps that researchers need to take in order to get the most out of their data. These include selecting appropriate extraction methods for identifying underlying factors and applying factor rotations to help clarify the factor structure.
Here are some of the key steps involved in conducting a successful EFA:
- Choose your extraction method: There are several different techniques available for extracting factors from your dataset, each with its own strengths and weaknesses. Some common options include principal axis factoring, maximum likelihood estimation, or minimum residuals (OLS) extraction. Depending on your specific research questions and needs, you may want to experiment with different methods until you find one that works best for you.
- Determine how many factors to extract: Once you’ve chosen an extraction method, it’s time to decide how many factors you want to extract from your dataset – this will depend on a variety of factors such as sample size and complexity of variables under consideration.
- Apply factor rotation: In order to better understand the relationships between our extracted factors (and avoid overfitting), we often apply factor rotation techniques like varimax or oblique rotation which can help us identify more meaningful patterns in our data by reducing noise and increasing clarity.
- Interpret results: Finally, once we’ve completed all these steps we can begin interpreting our results by looking at things like factor loadings, eigenvalues, scree plots etc., which can give us insight into what underlying structures might be driving our data.
As famed inventor Thomas Edison once said “Genius is 1% inspiration and 99% perspiration” – so too is success when using exploratory factor analysis!
Steps in Conducting an EFA
The below table summarizes the steps involved in conducting an EFA, including factor extraction, rotation, and interpretation. Use it as a reference guide when conducting your own EFA.
| Step | Description |
|---|---|
| Factor Extraction | Identify the number of factors to extract and conduct a preliminary factor analysis. |
| Factor Rotation | Rotate extracted factors to simplify the factor structure and increase interpretability. |
| Factor Interpretation | Interpret the final factor structure by examining factor loadings and identifying meaningful factor names. |
Sample Size and Sampling Adequacy for EFA
When it comes to conducting an exploratory factor analysis, one of the most important considerations is sample size and sampling adequacy. This is because if our sample size is too small, we may not have enough statistical power to detect meaningful relationships between variables in our data.
Similarly, if our measurement error or error variance is high (e.g., due to poor quality raw measurements), this can also reduce the accuracy of our results and make it harder to identify underlying factors. Therefore, when conducting EFA it’s important that we carefully consider both the quantity and quality of data used.
Fortunately, there are several ways we can test for sampling adequacy before proceeding with EFA. One popular technique involves calculating a statistic called Kaiser-Meyer-Olkin (KMO) which measures how well-suited your data is for factor analysis by examining the correlations between variables within your dataset.
Typically speaking, KMO values above 0.6 are considered adequate for EFA – although some researchers prefer higher thresholds depending on their research questions or goals. In addition to KMO values, you may also want to inspect other diagnostic measures like Bartlett’s test of sphericity which tests whether inter-correlations among variables are sufficiently different from zero so as not to be redundant with each other.
While sample size and sampling adequacy may seem like technical details at first glance – they’re actually incredibly important factors that can impact the validity and reliability of your study results! You’ll be better equipped than ever before to uncover hidden patterns within even complex datasets without worrying about issues related measurement error or inadequate sample sizes holding back your progress.
When conducting exploratory factor analysis, it’s critical to ensure that your sample size is adequate and that your sampling method is appropriate for the research question at hand. Consider factors such as the complexity of the data and the number of variables being analyzed when determining an appropriate sample size, and be sure to use a representative sample that accurately reflects the population you are studying.
Determining the Number of Factors in EFA
When conducting exploratory factor analysis, one of the most critical steps is determining the number of factors to extract from your data. This can be challenging since you may have multiple factors – both active and inactive – which make up your measured variables.
One approach researchers often use is examining a scree plot, which shows how many factors are needed to explain increasingly larger portions of variance in the dataset. In general, we’re looking for a bend or “elbow” point where adding additional factors no longer provides substantial gains in explanatory power.
Another technique that can be helpful is inspecting the eigenvalues associated with each factor. Essentially, these values represent how much variation in our data can be explained by each individual factor – with higher values indicating more important dimensions or patterns within our dataset.
Of course, it’s worth noting that there isn’t always a clear-cut answer when deciding on an optimal number of factors for EFA. Depending on your research questions and goals, extracting more (or fewer) dimensions may be appropriate! However, what’s important is that you carefully consider all available evidence before settling on any final conclusions about how many underlying components are present within your data.
Ultimately though, using techniques like scree plots and eigenvalue inspection can help us determine whether we need to extract 2-3 broad factors or dozens of narrow ones – reducing subjectivity and ensuring consistency across different datasets!
In practice then, determining the proper number of factors in EFA requires careful consideration along with some statistical intuition about which dimensions matter most within your particular study context. By weighing multiple pieces of evidence together (like scree plots and eigenvalues), you’ll be well-equipped to identify meaningful patterns within even complex datasets without getting bogged down by unnecessary details.
Methods for Determining the Number of Factors in EFA
This table shows commonly used methods for determining the number of factors in exploratory factor analysis, including Kaiser’s Rule, Scree Plot, and Parallel Analysis.
| Method | Description |
|---|---|
| Kaiser’s Rule | Retain all factors with eigenvalues greater than 1 |
| Scree Plot | Plot eigenvalues against factor number and retain the factors before the ‘elbow’ point |
| Parallel Analysis | Generate random data sets and compare eigenvalues to actual data eigenvalues to determine the number of factors to retain |
Interpreting EFA Results: Factor Loadings and Eigenvalues
As we continue to explore exploratory factor analysis, it’s essential to understand how to interpret the results obtained from this technique. Two of the most critical components that require careful attention include factor loadings and eigenvalues.
Firstly, factor loadings are essentially coefficients that represent how much each measured variable contributes towards a given latent variable or dimension. In other words, they tell us which variables are most strongly associated with specific factors within our data – allowing us to identify underlying patterns and relationships that might not be immediately apparent at first glance.
Moreover, these coefficients can help us gain insight into how different dimensions relate to each other – providing a more nuanced understanding of our data beyond what simple correlations can offer.
Secondly, eigenvalues also play a crucial role in EFA interpretation. These values indicate how much variation is explained by each latent variable or factor relative to all others included in the analysis.
Importantly though, since EFA typically produces multiple eigenvalues (one for every latent variable), it’s necessary to use some form of rotation method (e.g., varimax) when interpreting these results.
This process helps ensure that we’re only accounting for unique sources of variance across different dimensions rather than simply replicating information already captured by earlier factors.
Overall then, interpreting EFA results requires careful consideration of both factor loadings and eigenvalues, as well as an understanding of various statistical techniques like rotation methods. By examining these outputs together with your research questions and goals in mind, you’ll be able to gain deep insights into complex datasets without getting bogged down by unnecessary details!
Real-World Examples of Exploratory Factor Analysis
Real-world applications of exploratory factor analysis are widespread in fields like psychology, sociology, and marketing research. Such applications aim to identify potential factors that underlie complex datasets and provide a more nuanced understanding of the relationships between different variables.
For instance, in one study aimed at identifying predictors of job satisfaction among healthcare workers, EFA was used to analyze responses from multiple questionnaires. The statistical analysis revealed four distinct factors that were most strongly associated with overall job satisfaction: supervisor support, organizational culture, workload control, and staff empowerment.
Moreover, correlation coefficients obtained through EFA showed that these factors were highly interrelated – indicating the importance of considering multiple dimensions when examining employee well-being in this context.
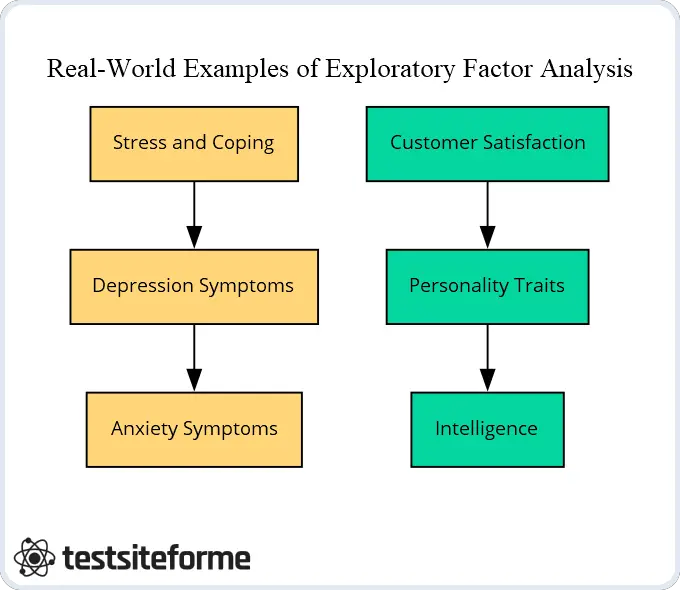
In another example from simulation studies involving large-scale data sets collected during clinical trials for depression treatment drugs. Researchers used EFA to identify latent variables underlying different aspects of depression symptomatology such as sadness or anhedonia (the inability to experience pleasure). They found evidence supporting a single factor representing general distress symptoms rather than several distinct ones related only to specific types of negative affectivity (e.g., anxiety).
These findings highlight how EFA can help uncover previously unknown patterns within complex data sets – ultimately leading researchers towards better-informed conclusions about their research question goals.
Advantages and Limitations of Exploratory Factor Analysis
Exploratory factor analysis has several advantages that make it a popular technique for analyzing complex data sets. For instance, EFA allows researchers to identify psychological factors underlying multiple observed variables – providing a more holistic understanding of how different aspects of the construct relate to each other.
Additionally, EFA can help uncover unique factors and idiosyncratic variances that may be missed using traditional statistical methods. By exploring these unique dimensions, researchers can gain new insights into complex phenomena such as personality traits or learning styles.
However, there are also some limitations associated with EFA. One potential issue is determining the appropriate number of factors in the analysis – which can be challenging if there are many highly correlated variables and no clear theoretical framework to guide selection.
Moreover, EFA assumes that observed variables have a linear relationship with underlying latent constructs – which may not always hold true in real-world data sets. Finally, maximum likelihood estimation used in exploratory factor analysis models requires large sample sizes to achieve accurate results; otherwise small samples may lead to unstable factor loadings or unreliable conclusions.
Despite these limitations, exploratory factor analysis remains an essential tool for discovering relationships among different measured variables and uncovering hidden structures within datasets. Whether applied in social sciences or market research contexts- it provides analysts with powerful insights into trends and patterns they might not have been able to discern otherwise.
To cut to the chase, while exploratory factor analysis isn’t perfect by any means- its benefits far outweigh its drawbacks when appropriately applied by informed practitioners who understand both its strengths and weaknesses alike.
Comparing EFA with Confirmatory Factor Analysis
When it comes to factor analysis, confirmatory factor analysis (CFA) is often compared to exploratory factor analysis. While both methods aim to identify latent factors that underlie observed variables, there are several differences between the two approaches.
Firstly, CFA tests a pre-determined model of the relationship between observed variables and underlying factors- while EFA allows researchers to explore how different variables might be related without any specific assumptions about correlation. This means that with CFA, analysts must have a clear theoretical framework in mind before conducting their analyses – whereas EFA can help generate hypotheses and theories for further testing.
Secondly, CFAs assume zero factor correlation unless explicitly specified in the model; whereas EFAs allow all pairs of factors to covary by default. One advantage of this assumption is that it helps minimize multicollinearity issues associated with highly correlated latent constructs.
Thirdly, while exploratory factor analysis uses polychoric correlations as input data when working with categorical or ordinal data types- CFA applies partial correlations on continuous phenotypes only.
Despite these differences in approach and methodology – both techniques are valuable psychological methods for uncovering relationships among hidden constructs within datasets. However, choosing which method works best depends on the specific research questions being asked and what type of data you’re working with: categorical vs continuous or theory-driven vs hypothesis-generating.
To reiterate, exploratory factor analysis enables researchers to explore complex patterns without a priori assumptions; confirmatory factor analyses require predetermined models but allow for more precise hypothesis testing given its explicit formulation. Both methods have their own strengths and weaknesses depending on what kind of problem you’re trying to solve!
Conclusion: When to Use Exploratory Factor Analysis in Research Projects
In social science research, exploratory factor analysis (EFA) is a useful tool for identifying underlying factors that drive the common variance among observed variables. EFA helps researchers to explore the relationships between different variables and analyze how they might be related in linear combinations.
One of the main advantages of EFA is its ability to identify latent constructs – such as personality traits or attitudes – that are not directly observable but may have significant impacts on behavior. By using EFA, researchers can uncover these hidden factors and better understand their role in shaping different outcomes.
Another benefit of EFA is its flexibility in handling various types of data – whether continuous or categorical. For instance, when working with categorical data like survey responses on a scale from 1-5, dummy variable techniques can be used to transform them into meaningful numerical values for further analysis.
However, it’s important to note that while exploratory factor analysis can reveal valuable insights into complex datasets- it should only be used as an exploratory tool and not relied upon solely for hypothesis testing or model validation due to its lack of predetermined theoretical framework assumptions like CFA has.
So when should you use exploratory factor analysis? If you want to uncover patterns among your observed variables without any preconceived notions about their relationships or need preliminary evidence before proceeding onto more rigorous methods then give exploratory factor analysis a try! Just remember that while it’s great at generating hypotheses; confirmatory factor analyses require predetermined models which allow more precise hypothesis testing given explicit formulation.








