Have you ever found yourself lost in a sea of statistical jargon, struggling to differentiate between parametric and nonparametric tests? Fear not, my friend – you are not alone. In the world of data analysis and research methodology, understanding the differences between these two types of tests is crucial for accurate interpretation and reporting of results.
At first glance, the terms “parametric” and “nonparametric” may seem daunting or even intimidating. However, they are simply different approaches to testing hypotheses about population parameters. Parametric tests assume that the data follows a specific distribution (usually normal) while nonparametric tests do not make any assumptions about the distribution.
In this article, we will explore the definitions and basic concepts of both types of tests, including their assumptions, advantages and limitations. We will also discuss practical examples and considerations for when to use each test. By the end of this article, you will have a comprehensive understanding of these tests and how to conduct them.
We will dive deeper into one-sample, two-sample, and paired samples tests as well as provide step-by-step guides on how to conduct both parametric and nonparametric tests with tips for successful analysis. Real-world applications will be explored through case studies and examples.
We’ll also address common misconceptions or pitfalls in using parametric vs nonparametric tests as well as hybrid approaches that combine both methods.
As we explore these topics together in this article, we hope to empower researchers, students, and professionals in statistics or data analysis with insights into future directions for these approaches so that they can stay ahead in their fields.
Parametric and Nonparametric Tests: Definitions and Basic Concepts
Parametric and nonparametric tests are two types of statistical analyses used to test hypotheses about population parameters. The main difference between these tests is that parametric tests require certain assumptions about the underlying distribution of the data, while nonparametric tests do not.
- Parametric Tests: These include t-tests, ANOVA, and correlation coefficient analysis. They assume that the data being analyzed follows a specific distribution (usually normal), and they rely on estimating parameters such as means and variances to make inferences about population characteristics. Parametric tests are generally more powerful than nonparametric tests when the assumptions are met, but can be less robust when those assumptions are violated.
- Nonparametric Tests: These include Wilcoxon rank-sum test, Kruskal-Wallis test, and Spearman’s rank correlation coefficient analysis. They make fewer assumptions about the distribution of the data being analyzed and use methods that do not involve parameter estimation or hypothesis testing based on distributional properties.
It is important to understand each type of test since choosing one over another can have significant implications for your research results.
When conducting spatial analysis or measuring growth rates in populations, it may be difficult to determine whether your data follows a normal distribution or any other specific type of distribution required by parametric testing. In such cases, non-parametrics might be a better choice because they don’t have strict requirements for input variables.
The bottom line is, understanding basic concepts like hypothesis testing is essential before diving into either method since both come with their advantages/disadvantages depending on what you’re trying to accomplish with your study design!
Assumptions of Parametric and Nonparametric Tests: What You Need to Know
Before conducting any statistical test, it is important to understand the assumptions that underlie parametric and nonparametric tests. These assumptions are critical because they affect the validity and reliability of your results. The main assumptions of parametric tests include homogeneity variance, normality distribution, independence observations, and equal sample size. On the other hand, nonparametric tests do not make many of these same assumptions.
Homogeneity variance assumes that the variability of data points across different groups or samples is similar. This assumption is necessary for some parametric tests such as t-tests and ANOVA since they rely on a common measure of variance across groups for accurate interpretation. Normality distribution refers to the assumption that data follows a bell-shaped curve called a normal distribution. This is also necessary for some parametric tests since they assume that data has a standard deviation and mean.
Independence observations assume that each measurement or observation in one group does not depend on another measurement in another group or set of measurements within its own group. This means there should be no correlation between measurements taken from different individuals or samples within each group.
Equal sample size assumes all groups being compared have an equal number of observations to prevent bias towards one particular group during analysis.
It’s worth noting that nonparametric methods do not necessarily require these same assumptions; instead, they rely on less stringent ones such as rank-ordering rather than requiring specific distributions or variances in their input data sets Therefore, understanding these assumptions can help you choose which type of test to use based on your research design while avoiding incorrect interpretations due to violated underlying principles.
Assumptions of Parametric and Nonparametric Tests
This table compares the assumptions of parametric and nonparametric tests, highlighting differences in the type of data they can handle and assumptions about normality and variance.
| Assumption | Parametric Test | Nonparametric Test |
|---|---|---|
| Type of Data | Continuous, normally distributed | Any type of data |
| Normality | Assumes normal distribution of data | Does not assume normal distribution of data |
| Variance | Assumes equal variance across groups | Does not assume equal variance across groups |
Advantages and Limitations of Parametric and Nonparametric Tests: Which One Should You Choose?
When it comes to choosing between parametric and nonparametric tests, there are several factors to consider. The advantages of parametric tests lie in their statistical power – they tend to be more sensitive and accurate when testing hypotheses about means and variances, assuming certain conditions are met. For instance, if you have normally distributed data with equal variances across groups, a t-test or ANOVA will likely yield more precise results than a nonparametric equivalent like the Wilcoxon rank-sum test or Kruskal-Wallis test. Another advantage of parametric tests is that they typically require smaller sample sizes than nonparametric tests to achieve the same level of significance.
On the other hand, the limitations of parametric tests stem from their assumptions about data distribution, which may not always hold true in practice. If your data is skewed or has outliers, for example, using a parametric test may lead to incorrect conclusions due to violations of normality or homoscedasticity assumptions. Nonparametric tests are generally more robust against such deviations from ideal conditions because they do not rely on specific probability distributions.
So which one should you choose? The answer depends on your research question, study design, and available resources. Here’s a summary of some key considerations:
Use parametric tests when:
- Your data follows a normal distribution
- You have equal variances across groups
- You want higher statistical power
- You have limited sample size
Use nonparametric tests when:
- Your data does not follow a normal distribution
- You have unequal variances across groups
- You want greater robustness against outliers or other anomalies
- Your sample size is large enough
Remember that these guidelines are not absolute rules – there may be situations where hybrid approaches or alternative methods (e.g., bootstrapping) could be better suited for your needs. Ultimately, the goal is to choose the most appropriate method for your specific research question while being aware of its strengths and weaknesses in relation to your data characteristics and analytical goals.
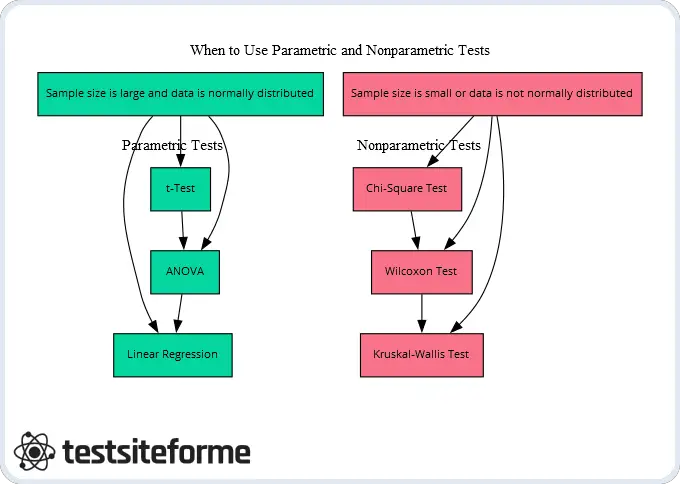
When to Use Parametric and Nonparametric Tests: Practical Examples and Considerations
When it comes to choosing between parametric and nonparametric tests, there are several practical examples and considerations to keep in mind. One major factor is whether your data meets the assumptions of a parametric test. These assumptions include normal distribution, equal variances, and independence of observations. If your data violates any of these assumptions, a nonparametric test may be more appropriate.
Another consideration is the type of analysis you need to conduct. For example, if you are interested in assessing the relationship between two continuous variables, you might use linear regression or correlation coefficient analysis – both of which are parametric tests. On the other hand, if you have categorical or ordinal data that cannot be transformed into interval-scale measurements (e.g., Likert scales), nonparametric tests like chi-squared or Mann-Whitney U might be more useful.
Here are some other practical examples and considerations for using parametric and nonparametric tests:
- ANOVA analysis: If you want to compare means across three or more groups (e.g., different treatment conditions), ANOVA is a common parametric test that assumes normal distribution of residuals.
- Paired samples t-test: This is a useful parametric test when comparing two related samples (e.g., pre-test vs post-test scores) with normally distributed differences.
- Wilcoxon signed-rank test: A nonparametric alternative for paired samples t-test used when the assumption of normality isn’t met.
- Kruskal-Wallis H Test: This non-parametrical can be used as an alternative for ANOVA when experimental condition’s residuals aren’t distributed normally
To put it briefly, understanding when to use each type of test requires careful consideration based on your research question and data characteristics. By selecting the right type of statistical method for your specific needs, you will increase your chances of obtaining accurate results that properly reflect your findings.
Understanding the Differences between One-Sample, Two-Sample, and Paired Samples Tests
When it comes to statistical analysis, one of the key distinctions between parametric and nonparametric tests is the type of data they are designed to handle. In particular, there are three main types of samples that researchers typically encounter: one-sample, two-sample, and paired samples. Each of these poses unique challenges for unpaired data analysis, matched samples comparison, single-sample hypothesis testing and independent population assessment.
One-sample tests involve comparing a sample mean or proportion to a known standard or population value. For example, suppose you want to test whether the average height of students in your school is significantly different from the national average. In this case, you would use a one-sample t-test or z-test depending on whether you know the standard deviation of heights in your school population.
Two-sample tests compare means or proportions from two independent groups that are not related in any way. For instance, if you want to compare the effectiveness of two different treatments on patients with a certain medical condition over time (e.g., before-and-after measurements), then you would need to conduct an unpaired t-test or z-test based on their respective means and variances.
Paired-samples tests involve comparing observations from two dependent groups that have been matched based on some criterion such as age, gender or treatment assignment. This type of comparison allows for more precise results by reducing variability due to individual differences between subjects. Common examples include pre- vs post-intervention measurements within individuals (e.g., blood pressure reading before and after taking medication) as well as sibling pairs who differ only by birth order (i.e., first-born vs second-born). To analyze such data sets statistically requires specialized techniques like paired t-tests which account for correlated errors across time points within each individual observation pair.
All in all, understanding when and how to use one-, two-, and paired-samples tests can make all the difference in conducting accurate statistical analyses with real-world applications across many fields including medicine business law social sciences engineering among others.
Characteristics and Appropriate Use of One-Sample, Two-Sample, and Paired Samples Tests
This table summarizes the differences between one-sample, two-sample, and paired samples tests and provides guidance on when to use each type of test.
| Test Type | Comparison | Assumptions | Appropriate Use |
|---|---|---|---|
| One-Sample | Sample mean vs. hypothesized value | Normality and homogeneity of variance | Testing whether a sample mean is significantly different from a known value |
| Two-Sample | Sample means from two independent groups | Normality and homogeneity of variance | Testing whether the means of two independent groups are significantly different from each other |
| Paired Samples | Sample means from two related groups | Normality and homogeneity of variance of the differences | Testing whether the means of two related groups (e.g. pre- and post-treatment) are significantly different from each other |
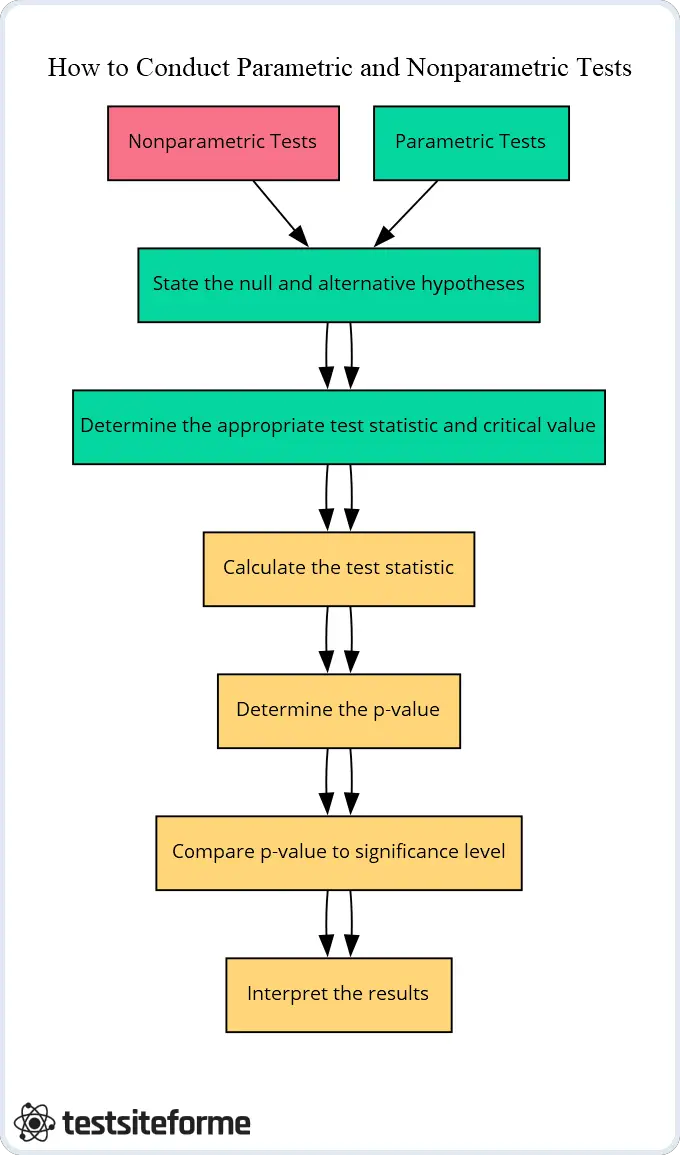
How to Conduct Parametric and Nonparametric Tests: Step-by-Step Guide and Tips
When it comes to conducting parametric and nonparametric tests, there are a few key steps you need to follow. First, you’ll want to determine which type of test is appropriate for your data analysis needs. This will depend on several factors, including the distribution of your data, the level of measurement of your variables, and the assumptions underlying each type of test.
Next, you’ll need to set up hypothesis testing procedures that will allow you to evaluate whether or not there is statistical significance in your findings. This involves specifying a null hypothesis (which assumes no significant effect) and an alternative hypothesis (which assumes that there is a significant effect).
Once these steps have been completed, it’s time to actually conduct the test. For parametric tests involving normally distributed data, this typically involves calculating a t-value or F-value using mathematical formulas based on means and standard deviations. Nonparametric tests may involve ranking observations or using other methods that do not rely on assumptions about normality.
To ensure accuracy in your results and minimize potential biases or errors in interpretation, it’s important to carefully follow established guidelines for conducting these types of tests. This may include checking for outliers or unusual values in your data, selecting appropriate sample sizes based on power calculations, and ensuring that all necessary assumptions are met before proceeding with analysis.
To cut through the noise, understanding how to conduct parametric vs nonparametric tests can be an essential tool for researchers who need reliable methods for evaluating statistical significance in their findings. By following best practices for data analysis and taking into account key considerations like distributional properties and measurement levels, you can help ensure accurate results while avoiding common pitfalls along the way.
Tips:
- Choose the appropriate test based on underlying assumptions
- Set up hypothesis testing procedures
- Conduct the test by calculating values
- Follow established guidelines
- Check for outliers
- Select appropriate sample sizes
Real-World Applications of Parametric and Nonparametric Tests: Case Studies and Examples
Real-world applications of parametric and nonparametric tests are vast and varied. These tests can be used to analyze data in various fields, including marketing analytics, medical research, education assessment, and environmental monitoring. Let’s take a closer look at some examples.
In marketing analytics, parametric tests can help businesses measure the effectiveness of their advertising campaigns by analyzing click-through rates or conversion rates. On the other hand, nonparametric tests can be useful in identifying consumer preferences based on survey responses or ratings.
Medical research often involves studying the effects of treatments or interventions on patient outcomes. Parametric tests are commonly used to compare means between two groups (e.g., treatment group versus control group) when certain assumptions about normality and equal variances are met. Nonparametric alternatives such as Wilcoxon rank-sum test may be preferred when these assumptions are not met or data is highly skewed.
Education assessment is another area where parametric and nonparametric tests have been applied extensively. For instance, t-tests can be used to determine if there is a significant difference in mean scores between two groups of students (e.g., those who received tutoring versus those who did not). Alternatively, nonparametric methods like Mann-Whitney U-test can also provide insights into differences between groups that may not satisfy normality assumptions.
Environmental monitoring encompasses processes involved in measuring physical parameters such as temperature or air quality over time across different locations. In this case, parametric tests like ANOVA (analysis of variance) could help detect spatial trends while accounting for temporal variation within each location separately. Non-parametrics like Kruskal-Wallis test might also prove useful when data does not meet the requirements for ANOVA assumptions.
To summarize – whether you’re analyzing click-through rates for an advertising campaign or studying the effects of a new medication on patient outcomes – understanding how to use both parametrics and non-parametrics will enhance your ability to draw meaningful conclusions from your data analysis results!
Before deciding whether to use a parametric or nonparametric test in your research, consider the nature of your data and the assumptions underlying each type of test. Don’t make assumptions based on convenience or familiarity; instead, choose the appropriate test for your specific research question and be prepared to defend your choice with sound reasoning and evidence. Remember, choosing the right statistical tests can mean the difference between accurate conclusions and misleading results.
Common Misconceptions and Pitfalls in Using Parametric and Nonparametric Tests
It’s easy to fall into common misconceptions and pitfalls when using parametric and nonparametric tests. One of the most prevalent mistakes is assuming that parametric tests always require a normality assumption for the data distribution. While many parametric tests do assume normality, there are exceptions such as t-tests with small sample sizes, which can tolerate deviations from normality to some extent.
Another misconception is assuming that nonparametric tests are always more robust than parametric tests. While it’s true that nonparametric tests don’t typically require assumptions about equal variances or underlying distributions, they can still have limitations in certain scenarios. For example, nonparametric tests may be less powerful than their parametric counterparts in detecting differences between groups, especially if the sample size is small or if there are ties in the data.
To avoid these misconceptions and pitfalls, it’s important to keep in mind some key tips:
- Always check whether your data meet the assumptions of each test before deciding which one to use.
- Consider using hybrid approaches that combine both types of tests to increase power and reduce type I error rate.
- Don’t rely solely on p-values; also consider effect sizes and confidence intervals when interpreting results.
By being aware of these issues and taking appropriate precautions, you can make better use of both parametric and nonparametric methods in your research or analysis.
Combining Parametric and Nonparametric Tests: Pros and Cons of Hybrid Approaches
Hybrid methods, also known as mixed models or combined approaches, are becoming increasingly popular in statistical analysis. These approaches combine elements of both parametric and nonparametric tests to provide more robust and flexible analyses. The main advantage of hybrid methods is that they allow for integrated analyses that can account for both the strengths and limitations of each approach.
One common example of a hybrid method is the use of nonparametric tests to validate or confirm the results obtained from parametric tests. This can be particularly useful when dealing with small sample sizes or data that do not meet the assumptions of normality or equal variances required by parametric tests. Another approach is to use mixed models that include both fixed and random effects, allowing for more nuanced analyses that can capture complex relationships between variables. To be brief, hybrid methods offer a range of options for researchers who want to take advantage of the benefits of both parametric and nonparametric approaches while minimizing their respective drawbacks.
Benefits:
- Provides more robust and flexible analyses
- Allows for integrated analyses
Drawbacks:
- Can be complex and time-consuming
- Requires careful consideration in selecting appropriate methods
Future Directions and Trends in Parametric and Nonparametric Tests: What to Expect
As we look towards the future of statistical analysis, there are several exciting developments on the horizon. One area that is poised to make a major impact is Bayesian inference, which allows for more flexible and accurate modeling of complex data sets. By incorporating prior knowledge and updating beliefs as new data becomes available, Bayesian methods can provide more robust estimates and better predictions than traditional frequentist approaches.
Another promising trend in statistical analysis is the growing use of machine learning algorithms. These powerful tools can handle vast amounts of data and identify patterns that might be difficult or impossible to detect with traditional methods. As machine learning continues to evolve, it is likely that it will become an increasingly important part of both parametric and nonparametric analyses.
In addition to these cutting-edge techniques, there are also ongoing efforts to improve the reliability and accuracy of existing methods. For example, researchers are developing new robust estimation procedures that can produce accurate results even in the presence of outliers or other sources of noise in the data.
Finally, multilevel modeling has emerged as a valuable tool for analyzing hierarchical data structures such as those found in social science research or medical studies. By accounting for variation at multiple levels (e.g., individual patients within hospitals), multilevel models can provide more nuanced insights into complex phenomena.
To reiterate, it’s clear that there are many exciting directions for future research in statistics and related fields. Whether you’re working with parametric or nonparametric tests – or some combination thereof – staying abreast of these trends will be essential for staying ahead in this rapidly evolving field.








