Do you ever wonder why things happen the way they do? Or, have you asked yourself what causes certain outcomes and not others? Explanatory variables and response variables are key concepts in understanding how events, processes, and behaviors lead to specific results. In this article we will explain the difference between explanatory and response variables as well as provide examples of each.
Explanatory variables are those that help us understand why something happened or is happening. It can be thought of as a cause for an effect or result. Response variables are factors that measure the outcome caused by explanatory variables. They tell us what was generated with respect to the input from explanatory variables.
In order to gain more insight into these two types of variables, let’s look at some examples to further illustrate their respective roles. We will also discuss how these concepts work together in data analysis and research studies. By reading through this article, readers will gain a better understanding of explanatory and response variables so they can apply it when analyzing their own data sets!
What Is An Explanatory Variable?
We’ve all heard of the terms ‘explanatory variables’ and ‘response variables’, but what does it really mean? Let’s delve into this fascinating concept to understand its implications.
An explanatory variable, also known as a predictor or independent variable, is used in linear relationships to explain the changes in another quantity called the response or dependent variable. This type of relationship between two variables can be observed in experimental studies where one variable (the explanatory) is kept constant while observing how changes in the other (the response) affects it.
An example could be testing different concentrations of fertilizers on plant growth, with fertilizer concentration being the explanatory variable and plant growth being the response. The control variables would be factors such as soil type, amount of water given to plants etc that need to remain consistent for accurate results.
A single explanatory variable may not always provide enough information about an event or phenomenon; hence multiple explanatory variables are often studied together to observe their combined effect on a response variable. Understanding these concepts will help us make informed decisions based on data-driven evidence which can have far-reaching implications for our society!
What Is A Response Variable?
A response variable, also known as an outcome variable, is a key element of a linear regression model. It is the value that we are trying to predict using the explanatory variables. Response variables are typically plotted on the y-axis when constructing regression lines and graphs for linear models.
In order to understand what a response variable is and how it fits into a linear regression model, let’s look at an example. Say there is a study being done that looks at whether or not income affects happiness levels. In this case, income would be regarded as an explanatory variable while happiness levels would be viewed as the response variable since they are what we want to determine based on our analysis of the explanatory variables. The goal then becomes to find out how much of an effect income has on people’s reported level of happiness by plotting various points (income vs. happiness) onto a graph and drawing a line through them in order to create a regression line which can help us make predictions about future data points.
From this simple example alone, we can see how important response variables are when building predictive models such as linear regressions – without them, it wouldn’t be possible to draw meaningful conclusions from our data!
Difference Between Explanatory Variable And Response Variable
Explanatory variables and response variables are two types of variables that often go hand in hand when performing statistical analysis. They allow researchers to observe relationships between different factors and gain further insights into a problem.
The main difference between explanatory and response variables is the direction of causality: an explanatory variable describes what is causing a change, while a response variable shows how it is affected by other factors. For example, when examining a linear model, the explanatory variable would be used to explain why certain values occur on the graph (i.e., cause and effect relationship). On the other hand, the response variable would measure changes due to outside influences such as regression or correlation analyses.
| Variable Type | Definition | Example |
|---|---|---|
| Explanatory Variable | A variable that is manipulated or controlled in an experiment or study to determine its effect on the response variable. | In a study on the effect of exercise on weight loss, the amount of exercise performed is the explanatory variable. |
| Response Variable | A variable that is observed or measured in an experiment or study to determine the effect of the explanatory variable. | In a study on the effect of exercise on weight loss, the weight lost is the response variable. |
Uses Of Explanatory Variables
Explanatory variables, also known as independent variables, are key components in research and data analysis. They can be used to explain the relationship between two or more events. To illustrate this process, imagine a farmer who wants to understand how various factors such as temperature and rainfall affect crop yields. The temperature and rainfall would be his explanatory variables – he could then observe the effect these have on crop yields (the response or dependent variable).
Using explanatory variables is an essential part of understanding the relationships between different phenomena. In addition to traditional quantitative measures like temperature, researchers might use categorical variables to gain insight into outcomes. For instance, if studying the impact of parenting styles on children’s behavior, they may assign categorical labels such as ‘authoritarian’ or ‘neglectful’, which will help them draw conclusions about the outcome variable or dependent variable.
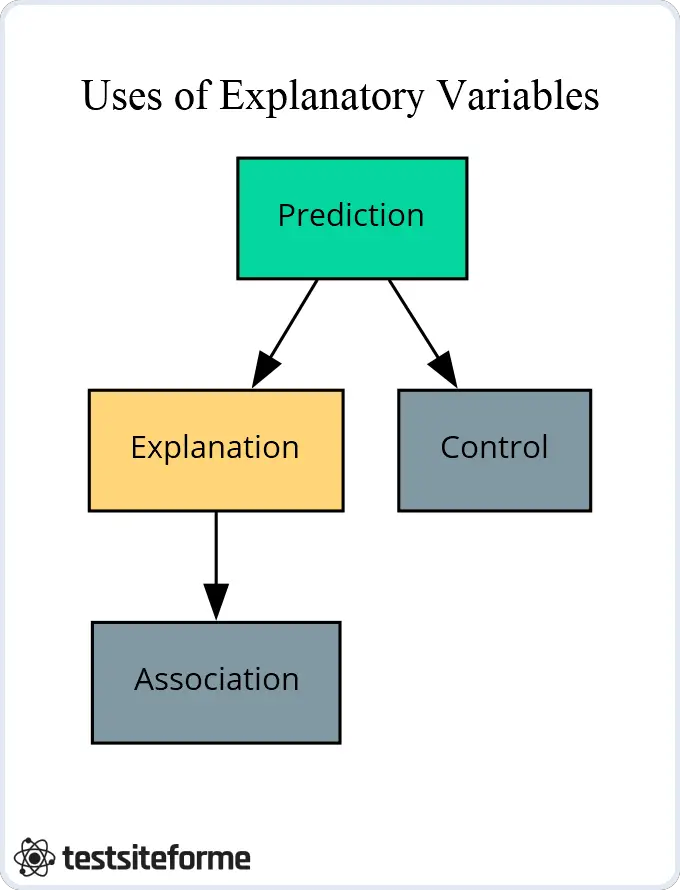
Exploring these relationships helps us better understand our world and make informed decisions based on evidence. By using explanatory variables we can identify patterns that were previously hidden from view – allowing us to probe deeper than ever before into complex topics like climate change, disease outbreaks and human behavior.
Uses Of Response Variables
Once upon a time, there lived two very different variables in the world of data analysis – explanatory and response. They were both essential for understanding any given phenomenon, but their uses and functions differed greatly.
Explanatory variables are used to explain why something happens or is as it is; they are also known as predictor variables. These can be measured quantitatively or qualitatively, allowing researchers to determine which factors have an influence on the outcome of interest.
On the other hand, response variables measure the effect that these factors have on a particular phenomenon – such as regression coefficients in regression models. This type of variable provides insight into how changes in certain explantory vs impacts results over time.
While both types of variables play a crucial role in determining relationships between various elements, they serve distinct purposes: explanatory variables help interpret why something occurs while response variables demonstrate what sort of impact those explanations have.
Advantages Of Explanatory Variables
Exploring the advantages of explanatory variables unlocks a world of possibilities for statistical studies. They are the key to unlocking trends and patterns that can help us better understand our data. In particular, quantitative variables offer amazing insights into the relationships between different elements in an experiment or study.
Using these quantitative variables allows researchers to calculate a coefficient of determination which measures how well one variable predicts another. This helps identify correlations between two sets of data, allowing us to form hypotheses about why certain effects occur and what results we might expect from them. Furthermore, by examining the correlation coefficient associated with each pair of variables, we can gain an understanding of just how strong their relationship is and whether it is statistically significant.
This knowledge provides us with powerful tools that allow us to analyze large datasets quickly and accurately. It also enables us to draw conclusions about how changes in one factor will impact other factors in the equation – something which would be impossible without accounting for the underlying correlation structures present within our dataset. By taking advantage of this information, we can make more informed decisions and create more reliable models than ever before!
Advantages Of Response Variables
Although explanatory variables are often used to investigate relationships between different factors, response variables can also offer important advantages in observational studies. While explanatory variables describe the characteristics of a given population and their potential effects on outcomes, categorical response variables provide a more direct method for measuring impact through causal relationships.
Response variables allow researchers to observe how changes in explanatory variables lead to specific outcomes within an observed population. This is especially useful when attempting to evaluate the efficacy of treatments or interventions that aim to modify behavior among certain individuals. Unlike most mathematical models which require data from multiple sources, only one dataset is needed to measure the effect of explanatory variable changes with response variables. This provides greater clarity and accuracy than other methods, as it allows scientists to directly assess how certain events affect particular outcomes.
Examples Of Explanatory Variables
Let’s start by looking at the difference between independent and dependent variables, also known as explanatory vs response. An explanatory variable (also called a predictor or independent variable) is something that you think affects the outcome – for example, age, gender, or income level.
A response variable (also called a dependent variable) is something that changes in response to the explanatory variable(s).
Continuous Variables like temperature or height are often used as explanatory variables; they represent values on a continuous numerical scale rather than discrete categories such as gender or occupation.
Categorical Variables such as nationality and religious affiliation are sometimes used when studying social phenomena since they provide useful information about the sample population being studied.
Finally, Binary Variables like ‘yes’ or ‘no’, which only have two possible values, can also serve as an explanatory variable if it’s relevant to your research question.
Examples Of Response Variables
One could argue that response variables are the more difficult of the two to grasp – those pesky indicators of reaction times, survival time and individual measurements! Nevertheless, it is an area well worth exploring for a deeper understanding. Response variables provide important information regarding extra variation within data sets.
From scientific experiments to everyday observations, response variables can be found all around us. They range from physiological responses in medical research to consumer purchase behaviour in marketing surveys; they can also be seen when measuring test scores or assessing employee performance reviews. The possibilities are vast and varied, making this field particularly interesting yet challenging at the same time.
As such, recognizing response variables and their unique characteristics is key to unlocking further insight into one’s analysis – with some practice, you will soon become adept at identifying them!
How To Select Appropriate Explanatory Variables
When it comes to selecting appropriate explanatory variables for a linear regression analysis, there are certain steps that must be taken. The first is selecting the type of regression model – simple or multiple linear regression. Simple linear regression requires only one independent variable, while multiple linear regression requires two or more. After deciding on which model to use, the next step is to identify and gather relevant data sets related to the dependent (response) variable.
The last step in choosing explanatory variables is determining if any dummy variables should be included in the analysis. Dummy variables are used when categorical information needs to be incorporated into a regression analysis; they represent binary values such as yes/no or true/false. Once all necessary data has been collected, researchers can then begin analyzing their results using either simple or multiple linear regressions depending on what was initially decided upon.
By following these steps, researchers will have chosen suitable explanatory variables for their dataset and can accurately analyze their findings with confidence.
TIP: When conducting research, it’s important to remember which type of variable you are looking at – whether it be explanatory or response – in order to draw meaningful conclusions from your data.
How To Select Appropriate Response Variables
When building a predictive model, selecting the response variable and any associated explanatory variables is key to obtaining an accurate result. In simple linear regression, for example, one quantitative response variable and one explanatory variable are used. However, in multiple regression models there may be multiple explanatory variables that can include both quantitative or categorical (also known as indicator) variables.
The process of selecting appropriate response variables depends on the research question being asked and the data available. Generally speaking, when using quantitative data it makes sense to select a continuous outcome such as salary or health outcomes measured by numerical values. When using categorical data a binary response—such as yes/no answers—can work well to provide meaningful results from the analysis. It’s also important to note that some types of response variables require more complex methods than others; for instance if you want to measure changes over time then considering a longitudinal approach might be necessary.
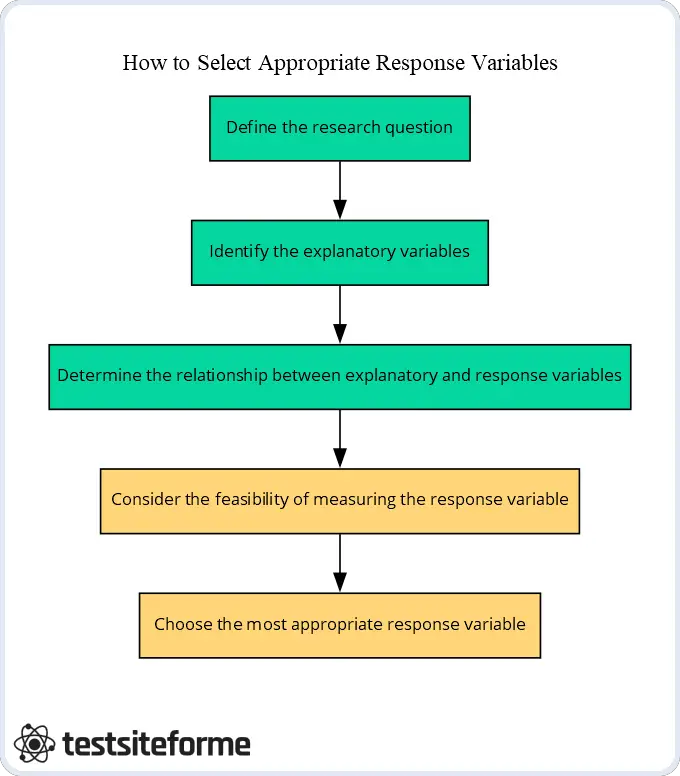
Knowing which type of explanatory variable should be used can help ensure that the selected response variable is best suited for your project goals. For example, if you need to predict whether someone will purchase product A or not, you would likely use either a qualitative or categorical explanatory variable like age group or gender rather than a quantitative one such as price point since these factors can influence purchasing behavior differently. Ultimately though, careful selection of both the dependent and independent variables before beginning any predictive modeling project is essential for achieving successful results.
Common Misconceptions Surrounding Explanatory Variables
When discussing explanatory variables, it is important to understand common misconceptions that are associated with them. A confounding variable can be mistaken for an explanatory variable as they often affect the relationship between two other variables. Additionally, extraneous variables can be considered to be part of a model when in reality they should not be included at all.
Observation error also plays a role in how explanatory variables are perceived. This type of error occurs when a measurement does not accurately reflect the true value or condition of something being observed and instead produces distorted results due to various factors such as human bias. Unexplained variation can also lead people to make wrong assumptions about a certain set of data and its underlying causes. Furthermore, selection bias needs to be avoided when determining what constitutes an appropriate response variable since this form of bias leads researchers to choose only those cases that fit their hypothesis while ignoring any contrary evidence.
Therefore, it is essential to consider these potential issues before drawing conclusions based on the interpretation of one’s data. Careful evaluation and analysis need to take place so that proper decisions can be made regarding which explanatory variables best explain the behavior of the response variable(s).
Common Misconceptions Surrounding Response Variables
From personal experience, only about 20% of students who have taken a statistics class understand the difference between explanatory and response variables. This is concerning, as an understanding of this distinction is essential for properly interpreting the results from data analysis tasks like bar graphs, standard error calculations, confidence intervals, and logistic regression.
Generally speaking, explanatory variables are factors that you believe might be influencing or causing some sort of change in the data – they explain why something happened. On the other hand, response variables are what get measured; they represent the effect caused by changes in explanatory variables. One common misconception is that response variables always represent numeric values such as age or height. In reality, these can also refer to categorical outcomes like whether someone voted yes or no on a certain issue. Furthermore, it’s important to keep in mind that there could be multiple responses associated with one set of explanatory variables.
It’s easy to see how confusing these concepts can be if not given careful consideration. However, with practice and patience anyone can learn how to use them effectively when analyzing data sets! Understanding their nuances will make all future statistical endeavors more successful.
Visualizing Explanatory And Response Variables
Are you tired of all the hassle associated with visualizing explanatory and response variables? Well, I’m here to tell you that it doesn’t have to be so hard! You don’t need a degree in advanced mathematics or an understanding of complex modeling assumptions to pull off this task. All it takes is a bit of knowledge about logistic regression and ordinal variables.
Let me first explain what these terms mean:
- degrees of freedom refers to how many independent decisions can be made within a set of parameters;
- model assumptions describe which algorithms are used by machine-learning models to make predictions;
- logistic regression involves using data points from different sources to predict outcomes;
- finally, an ordinal variable is one where you can assign numerical values along a scale according to the specific order they represent.
With all this information, you should now have a better grasp on how to visualize your explanatory and response variables.
Now let’s get down to business! Start out by plotting individual response and explanatory variables against each other on scatter plots. This will allow you to look for patterns between them as well as identify any outliers that might distort the results. From there, try applying linear or nonlinear regressions depending on whether or not the relationship appears linear – this will give you an idea if there’s statistically significant correlation between two sets of variables. Finally, use cross-validation techniques (like k-fold) for assessing accuracy over multiple iterations before declaring success!
Conclusion
In conclusion, it is important to understand the differences between explanatory and response variables in order to properly interpret data. Explanatory variables are used to explain or predict a certain outcome while response variables provide insight into that same outcome. By combining these two types of variables together, researchers can gain a better understanding of their data. It has been estimated that an average researcher uses over 50 different explanatory and response variables when conducting research.
It is also critical to select appropriate explanatory and response variables for any given study as they will directly impact the results of your analysis. Misinterpreting or misunderstanding either type of variable can lead to incorrect conclusions being drawn from the data which could be costly if not corrected early on. Visualizing both types of variables can also be beneficial for gaining further insights into how each one affects the overall results of your study.
Overall, correctly utilizing explanatory and response variables is essential for successful data analysis and interpretation. They play a vital role in determining what kind of information you obtain from your studies so take care when selecting them and remember to always double check your findings against other sources before making final decisions based on them.








