Ti sei mai trovato perso in un mare di gergo statistico, lottando per differenziare tra test parametrici e non parametrici? Non temere, amico mio – non sei solo. Nel mondo dell’analisi dei dati e della metodologia di ricerca, comprendere le differenze tra questi due tipi di test è cruciale per un’interpretazione e una segnalazione accurata dei risultati.
A prima vista, i termini “parametrico” e “non parametrico” possono sembrare intimidatori o persino spaventosi. Tuttavia, sono semplicemente approcci diversi per testare le ipotesi sui parametri della popolazione. I test parametrici assumono che i dati seguano una distribuzione specifica (di solito normale), mentre i test non parametrici non fanno alcuna supposizione sulla distribuzione.
In questo articolo, esploreremo le definizioni e i concetti di base di entrambi i tipi di test, compresi i loro presupposti, vantaggi e limitazioni. Discuteremo anche esempi pratici e considerazioni su quando utilizzare ciascun test. Alla fine di questo articolo, avrai una comprensione completa di questi test e di come condurli.
Approfondiremo i test su campioni singoli, su due campioni e su campioni accoppiati e forniremo guide passo-passo su come condurre sia test parametrici che non parametrici con suggerimenti per un’analisi di successo. Le applicazioni del mondo reale saranno esplorate attraverso studi di caso ed esempi.
Affronteremo anche i comuni fraintendimenti o le trappole nell’uso di test parametrici vs non parametrici, nonché approcci ibridi che combinano entrambi i metodi.
Mentre esploriamo questi argomenti insieme in questo articolo, speriamo di dare potere ai ricercatori, agli studenti e ai professionisti in statistica o analisi dei dati con intuizioni sulle future direzioni per questi approcci in modo che possano rimanere avanti nei loro campi.
Test parametrici e non parametrici: definizioni e concetti di base
I test parametrici e non parametrici sono due tipi di analisi statistiche utilizzate per testare le ipotesi sui parametri della popolazione. La principale differenza tra questi test è che i test parametrici richiedono determinate ipotesi sulla distribuzione sottostante dei dati, mentre i test non parametrici no.
- Test parametrici: Questi includono i test t, ANOVA e l’analisi del coefficiente di correlazione. Assumono che i dati analizzati seguano una distribuzione specifica (solitamente normale) e si basano sulla stima dei parametri come medie e varianze per fare inferenze sulle caratteristiche della popolazione. I test parametrici sono generalmente più potenti dei test non parametrici quando le ipotesi sono soddisfatte, ma possono essere meno robusti quando tali ipotesi vengono violate.
- Test non parametrici: Questi includono il test di Wilcoxon, il test di Kruskal-Wallis e l’analisi del coefficiente di correlazione di Spearman. Fanno meno ipotesi sulla distribuzione dei dati analizzati e utilizzano metodi che non implicano la stima dei parametri o l’ipotesi di prova basate sulle proprietà distributive.
È importante capire ogni tipo di test poiché sceglierne uno rispetto all’altro può avere implicazioni significative per i risultati della ricerca.
Nell’analisi spaziale o nella misurazione dei tassi di crescita delle popolazioni, potrebbe essere difficile determinare se i dati seguono una distribuzione normale o qualsiasi altro tipo di distribuzione specifica richiesta dai test parametrici. In tali casi, i test non parametrici potrebbero essere una scelta migliore poiché non hanno requisiti rigidi per le variabili di input.
In definitiva, capire concetti di base come la prova delle ipotesi è essenziale prima di immergersi in uno dei due metodi poiché entrambi hanno vantaggi/svantaggi a seconda di ciò che si cerca di ottenere con il proprio progetto di studio!
Assunzioni dei test parametrici e non parametrici: ciò che devi sapere
Prima di condurre qualsiasi test statistico, è importante comprendere le assunzioni che sottostanno ai test parametrici e non parametrici. Queste assunzioni sono cruciali perché influenzano la validità e l’affidabilità dei tuoi risultati. Le principali assunzioni dei test parametrici includono la varianza di omogeneità, la distribuzione di normalità, le osservazioni indipendenti e le dimensioni campionarie uguali. D’altra parte, i test non parametrici non fanno molte di queste stesse assunzioni.
La varianza di omogeneità assume che la variabilità dei punti dati tra diversi gruppi o campioni sia simile. Questa assunzione è necessaria per alcuni test parametrici come i test t e ANOVA poiché si basano su una misura comune della varianza tra i gruppi per una corretta interpretazione. La distribuzione di normalità si riferisce all’assunzione che i dati seguano una curva a forma di campana chiamata distribuzione normale. Questo è anche necessario per alcuni test parametrici poiché assumono che i dati abbiano una deviazione standard e una media.
Le osservazioni indipendenti assumono che ogni misurazione o osservazione in un gruppo non dipenda da un’altra misurazione in un altro gruppo o insieme di misurazioni all’interno del proprio gruppo. Ciò significa che non dovrebbe esserci alcuna correlazione tra le misurazioni prese da diversi individui o campioni all’interno di ciascun gruppo.
Le dimensioni campionarie uguali assumono che tutti i gruppi confrontati abbiano lo stesso numero di osservazioni per evitare un bias verso un particolare gruppo durante l’analisi.
È importante notare che i metodi non parametrici non richiedono necessariamente queste stesse assunzioni; invece, si basano su assunzioni meno rigorose come l’ordinamento per rango anziché richiedere distribuzioni o varianze specifiche nei loro set di dati di input. Pertanto, comprendere queste assunzioni può aiutarti a scegliere quale tipo di test utilizzare in base al tuo design di ricerca evitando interpretazioni errate a causa di principi sottostanti violati.
Assunzioni dei test parametrici e non parametrici
Questa tabella confronta le assunzioni dei test parametrici e non parametrici, evidenziando le differenze nel tipo di dati che possono gestire e le assunzioni sulla normalità e sulla varianza.
| Assunzione | Test parametrico | Test non parametrico |
|---|---|---|
| Tipo di dati | Continuo, distribuito normalmente | Qualsiasi tipo di dato |
| Normalità | Assume la distribuzione normale dei dati | Non assume la distribuzione normale dei dati |
| Varianza | Assume la varianza uguale tra i gruppi | Non assume la varianza uguale tra i gruppi |
Vantaggi e Limitazioni dei Test Parametrici e Nonparametrici: Quale Scegliere?
Quando si tratta di scegliere tra test parametrici e nonparametrici, ci sono diversi fattori da considerare. I vantaggi dei test parametrici risiedono nella loro potenza statistica – tendono ad essere più sensibili e precisi quando si testano ipotesi su medie e varianze, assumendo che siano soddisfatte determinate condizioni. Ad esempio, se si hanno dati distribuiti normalmente con varianze uguali tra i gruppi, un test t o ANOVA probabilmente fornirà risultati più precisi rispetto a un equivalente nonparametrico come il test di Wilcoxon o il test di Kruskal-Wallis. Un altro vantaggio dei test parametrici è che di solito richiedono campioni più piccoli rispetto ai test nonparametrici per raggiungere lo stesso livello di significatività.
D’altra parte, le limitazioni dei test parametrici derivano dalle loro assunzioni sulla distribuzione dei dati, che potrebbero non essere sempre vere nella pratica. Se i dati sono asimmetrici o hanno valori anomali, ad esempio, l’utilizzo di un test parametrico potrebbe portare a conclusioni errate a causa di violazioni delle assunzioni di normalità o omoschedasticità. I test nonparametrici sono generalmente più robusti contro tali deviazioni dalle condizioni ideali perché non si basano su specifiche distribuzioni di probabilità.
Quale scegliere? La risposta dipende dalla domanda di ricerca, dal disegno dello studio e dalle risorse disponibili. Ecco un riassunto di alcune considerazioni chiave:
Utilizza i test parametrici quando:
- I tuoi dati seguono una distribuzione normale
- Hai varianze uguali tra i gruppi
- Vuoi una maggiore potenza statistica
- Hai un campione limitato
Utilizza i test nonparametrici quando:
- I tuoi dati non seguono una distribuzione normale
- Hai varianze diverse tra i gruppi
- Vuoi una maggiore robustezza contro valori anomali o altre anomalie
- Il tuo campione è abbastanza grande
Ricorda che queste linee guida non sono regole assolute – potrebbero esserci situazioni in cui approcci ibridi o metodi alternativi (ad esempio, il bootstrapping) potrebbero essere più adatti alle tue esigenze. In definitiva, l’obiettivo è scegliere il metodo più appropriato per la tua specifica domanda di ricerca, tenendo conto dei suoi punti di forza e di debolezza in relazione alle caratteristiche dei tuoi dati e agli obiettivi analitici.
Quando utilizzare test parametrici e non parametrici: esempi pratici e considerazioni
Quando si tratta di scegliere tra test parametrici e non parametrici, ci sono diversi esempi pratici e considerazioni da tenere a mente. Un fattore importante è se i dati soddisfano le ipotesi di un test parametrico. Queste ipotesi includono la distribuzione normale, le varianze uguali e l’indipendenza delle osservazioni. Se i dati violano una qualsiasi di queste ipotesi, potrebbe essere più appropriato utilizzare un test non parametrico.
Un’altra considerazione è il tipo di analisi che si deve condurre. Ad esempio, se si è interessati a valutare la relazione tra due variabili continue, potrebbe essere utilizzato un’analisi di regressione lineare o un coefficiente di correlazione, entrambi test parametrici. D’altra parte, se si hanno dati categorici o ordinali che non possono essere trasformati in misurazioni su scala intervallo (ad esempio, scale Likert), test non parametrici come il chi quadrato o il test di Mann-Whitney U potrebbero essere più utili.
Ecco alcuni altri esempi pratici e considerazioni per l’utilizzo di test parametrici e non parametrici:
- Analisi ANOVA: se si desidera confrontare le medie tra tre o più gruppi (ad esempio, diverse condizioni di trattamento), l’ANOVA è un comune test parametrico che assume la distribuzione normale dei residui.
- T-test per campioni accoppiati: questo è un utile test parametrico quando si confrontano due campioni correlati (ad esempio, punteggi pre-test vs post-test) con differenze distribuite normalmente.
- Test di Wilcoxon: un’alternativa non parametrica al t-test per campioni accoppiati utilizzata quando l’ipotesi di normalità non è soddisfatta.
- Test di Kruskal-Wallis H: questo test non parametrico può essere utilizzato come alternativa all’ANOVA quando i residui delle condizioni sperimentali non sono distribuiti normalmente.
In breve, capire quando utilizzare ciascun tipo di test richiede una attenta considerazione basata sulla domanda di ricerca e le caratteristiche dei dati. Se si seleziona il tipo giusto di metodo statistico per le proprie esigenze specifiche, si aumenteranno le possibilità di ottenere risultati accurati che riflettono correttamente le proprie scoperte.
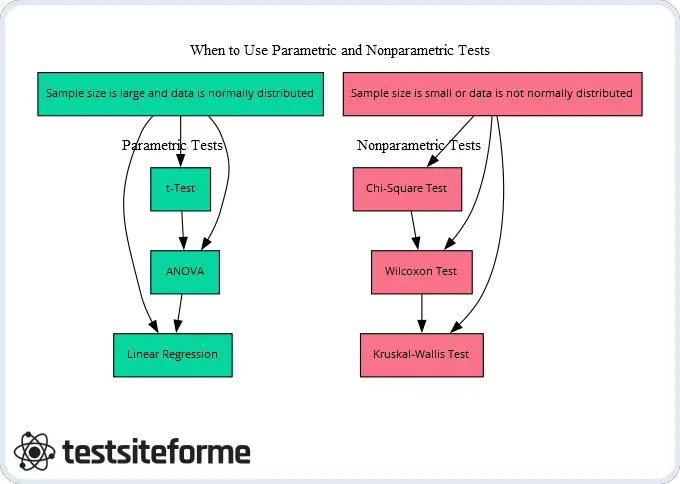
Comprensione delle differenze tra test di campione singolo, test di due campioni e test di campioni accoppiati
Per quanto riguarda l’analisi statistica, una delle distinzioni chiave tra i test parametrici e non parametrici è il tipo di dati che sono progettati per gestire. In particolare, ci sono tre tipi principali di campioni che i ricercatori incontrano tipicamente: campione singolo, due campioni e campioni accoppiati. Ciascuno di questi presenta sfide uniche per l’analisi dei dati non accoppiati, il confronto di campioni accoppiati, il testing dell’ipotesi a campione singolo e la valutazione della popolazione indipendente.
I test di campione singolo implicano il confronto di una media o proporzione del campione con un valore noto o di popolazione. Ad esempio, supponiamo che si voglia testare se l’altezza media degli studenti nella propria scuola è significativamente diversa dalla media nazionale. In questo caso, si utilizzerebbe un test t o z a campione singolo a seconda che si conosca la deviazione standard delle altezze nella propria popolazione scolastica.
I test di due campioni confrontano le medie o le proporzioni di due gruppi indipendenti che non sono correlati in alcun modo. Ad esempio, se si vuole confrontare l’efficacia di due diversi trattamenti su pazienti con una determinata condizione medica nel tempo (ad esempio, misurazioni prima e dopo), allora si dovrebbe condurre un test t o z non accoppiato basato sulle rispettive medie e varianze.
I test di campioni accoppiati implicano il confronto di osservazioni da due gruppi dipendenti che sono stati accoppiati in base a qualche criterio come l’età, il genere o l’assegnazione del trattamento. Questo tipo di confronto consente risultati più precisi riducendo la variabilità dovuta alle differenze individuali tra i soggetti. Esempi comuni includono le misurazioni pre- vs post-intervento all’interno di singoli individui (ad esempio, la lettura della pressione sanguigna prima e dopo l’assunzione di farmaci) e coppie di fratelli che differiscono solo per l’ordine di nascita (cioè primogeniti vs secondogeniti). Per analizzare tali set di dati statisticamente, sono necessarie tecniche specializzate come i test t accoppiati che tengono conto degli errori correlati nel tempo in ciascuna coppia di osservazioni individuali.
In generale, comprendere quando e come utilizzare i test di campione singolo, di due campioni e di campioni accoppiati può fare la differenza nell’effettuare analisi statistiche accurate con applicazioni reali in molti campi, tra cui medicina, business, legge, scienze sociali, ingegneria, tra gli altri.
Caratteristiche e uso appropriato dei test di campione singolo, di due campioni e di campioni accoppiati
Questa tabella riassume le differenze tra i test di campione singolo, di due campioni e di campioni accoppiati e fornisce indicazioni su quando utilizzare ciascun tipo di test.
| Tipo di test | Confronto | Assunzioni | Uso appropriato |
|---|---|---|---|
| Campione singolo | Media del campione vs valore ipotizzato | Normalità e omogeneità della varianza | Testare se una media del campione è significativamente diversa da un valore noto |
| Due campioni | Medie del campione di due gruppi indipendenti | Normalità e omogeneità della varianza | Testare se le medie di due gruppi indipendenti sono significativamente diverse tra loro |
| Campioni accoppiati | Medie del campione di due gruppi correlati | Normalità e omogeneità della varianza delle differenze | Testare se le medie di due gruppi correlati (ad esempio, pre- e post-trattamento) sono significativamente diverse tra loro |
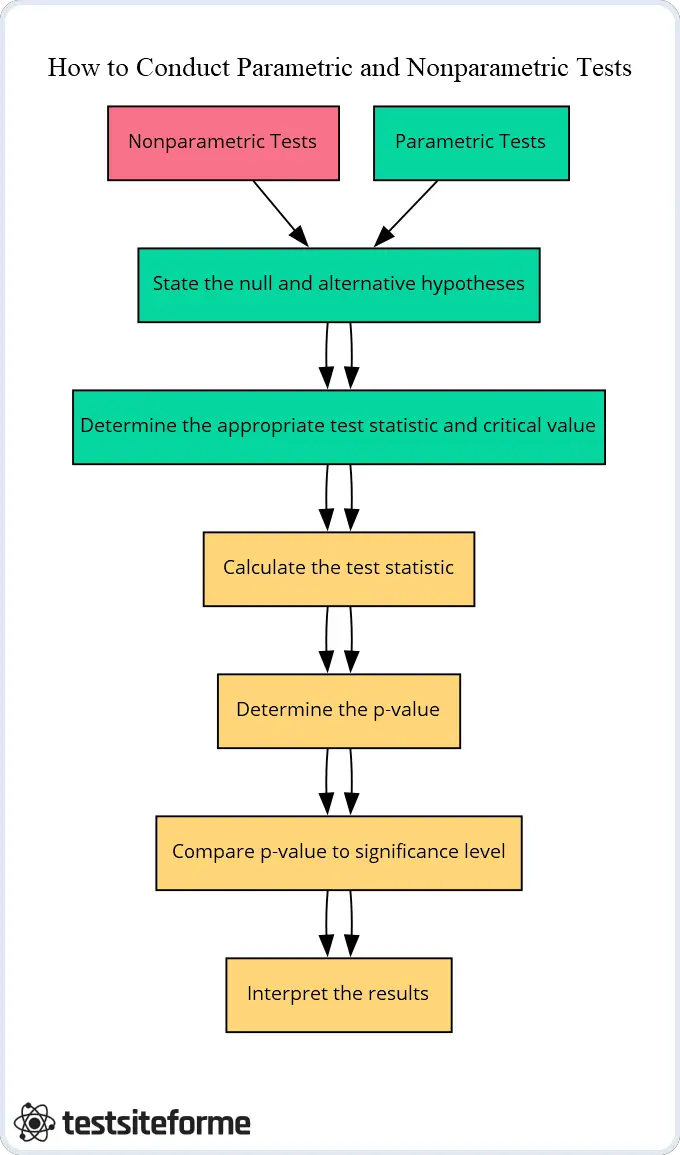
Come Condurre Test Parametrici e Non Parametrici: Guida Passo-Passo e Consigli
Quando si tratta di condurre test parametrici e non parametrici, ci sono alcuni passaggi chiave che è necessario seguire. In primo luogo, è necessario determinare quale tipo di test sia appropriato per le proprie esigenze di analisi dei dati. Ciò dipenderà da diversi fattori, tra cui la distribuzione dei dati, il livello di misurazione delle variabili e le assunzioni alla base di ciascun tipo di test.
Successivamente, sarà necessario impostare le procedure di test di ipotesi che consentiranno di valutare se ci sia o meno una significatività statistica nei propri risultati. Ciò comporta la specifica di un’ipotesi nulla (che assume l’assenza di un effetto significativo) e un’ipotesi alternativa (che assume l’esistenza di un effetto significativo).
Una volta completati questi passaggi, è il momento di condurre effettivamente il test. Per i test parametrici che coinvolgono dati distribuiti normalmente, ciò comporta tipicamente il calcolo di un valore t o F utilizzando formule matematiche basate su medie e deviazioni standard. I test non parametrici possono comportare il ranking delle osservazioni o l’utilizzo di altri metodi che non si basano su assunzioni di normalità.
Per garantire l’accuratezza dei propri risultati e minimizzare i potenziali bias o errori di interpretazione, è importante seguire attentamente le linee guida stabilite per la conduzione di questi tipi di test. Ciò può includere la verifica di valori anomali o insoliti nei propri dati, la selezione di dimensioni campionarie appropriate in base ai calcoli di potenza e la verifica che tutte le assunzioni necessarie siano soddisfatte prima di procedere con l’analisi.
Per tagliare la confusione, comprendere come condurre test parametrici vs non parametrici può essere uno strumento essenziale per i ricercatori che hanno bisogno di metodi affidabili per valutare la significatività statistica dei propri risultati. Seguendo le migliori pratiche per l’analisi dei dati e tenendo conto di considerazioni chiave come le proprietà distributive e i livelli di misurazione, si può contribuire a garantire risultati accurati evitando le comuni insidie lungo il percorso.
Consigli:
- Scegliere il test appropriato in base alle assunzioni sottostanti
- Impostare le procedure di test di ipotesi
- Condurre il test calcolando i valori
- Seguire le linee guida stabilite
- Verificare la presenza di valori anomali
- Selezionare dimensioni campionarie appropriate
Applicazioni reali di test parametrici e non parametrici: studi di caso ed esempi
Le applicazioni reali di test parametrici e non parametrici sono molteplici e variegate. Questi test possono essere utilizzati per analizzare dati in diversi campi, tra cui l’analisi del marketing, la ricerca medica, la valutazione dell’istruzione e il monitoraggio ambientale. Vediamo alcuni esempi più da vicino.
Nell’analisi del marketing, i test parametrici possono aiutare le aziende a misurare l’efficacia delle loro campagne pubblicitarie analizzando i tassi di click o di conversione. Al contrario, i test non parametrici possono essere utili per identificare le preferenze dei consumatori in base alle risposte ai sondaggi o alle valutazioni.
La ricerca medica spesso comporta lo studio degli effetti dei trattamenti o delle interventi sui risultati dei pazienti. I test parametrici sono comunemente utilizzati per confrontare le medie tra due gruppi (ad esempio, il gruppo di trattamento rispetto al gruppo di controllo) quando vengono soddisfatte determinate ipotesi sulla normalità e la varianza uguale. Le alternative non parametriche come il test di Wilcoxon a due campioni possono essere preferite quando queste ipotesi non sono soddisfatte o i dati sono fortemente asimmetrici.
La valutazione dell’istruzione è un altro campo in cui i test parametrici e non parametrici sono stati ampiamente applicati. Ad esempio, i test t possono essere utilizzati per determinare se esiste una differenza significativa nei punteggi medi tra due gruppi di studenti (ad esempio, quelli che hanno ricevuto il tutoraggio rispetto a quelli che non l’hanno fatto). In alternativa, i metodi non parametrici come il test di Mann-Whitney U possono anche fornire informazioni sulle differenze tra i gruppi che potrebbero non soddisfare le ipotesi di normalità.
Il monitoraggio ambientale comprende i processi coinvolti nella misurazione di parametri fisici come la temperatura o la qualità dell’aria nel tempo in diverse posizioni. In questo caso, i test parametrici come l’ANOVA (analisi della varianza) potrebbero aiutare a rilevare tendenze spaziali tenendo conto della variazione temporale in ciascuna posizione separatamente. I non parametrici come il test di Kruskal-Wallis potrebbero anche risultare utili quando i dati non soddisfano i requisiti per le ipotesi dell’ANOVA.
In sintesi, che si stia analizzando i tassi di click per una campagna pubblicitaria o studiando gli effetti di un nuovo farmaco sui risultati dei pazienti, comprendere come utilizzare sia i test parametrici che non parametrici migliorerà la capacità di trarre conclusioni significative dai risultati dell’analisi dei dati!
Prima di decidere se utilizzare un test parametrico o non parametrico nella propria ricerca, è importante considerare la natura dei propri dati e le ipotesi sottostanti a ciascun tipo di test. Non fare supposizioni basate sulla convenienza o la familiarità; invece, scegliere il test appropriato per la propria specifica domanda di ricerca e essere preparati a difendere la propria scelta con un ragionamento e una prova solida. Ricorda, scegliere i giusti test statistici può fare la differenza tra conclusioni accurate e risultati fuorvianti.
Comuni fraintendimenti e insidie nell’uso di test parametrici e non parametrici
È facile cadere in comuni fraintendimenti e insidie quando si utilizzano test parametrici e non parametrici. Uno degli errori più diffusi è assumere che i test parametrici richiedano sempre un’assunzione di normalità per la distribuzione dei dati. Sebbene molti test parametrici presuppongano la normalità, ci sono eccezioni come i test t con piccole dimensioni del campione, che possono tollerare deviazioni dalla normalità in una certa misura.
Un altro fraintendimento è assumere che i test non parametrici siano sempre più robusti dei test parametrici. Sebbene sia vero che i test non parametrici di solito non richiedano assunzioni sulla varianza uguale o sulle distribuzioni sottostanti, possono ancora avere limitazioni in determinati scenari. Ad esempio, i test non parametrici possono essere meno potenti dei loro omologhi parametrici nel rilevare differenze tra gruppi, soprattutto se la dimensione del campione è piccola o se ci sono legami nei dati.
Per evitare questi fraintendimenti e insidie, è importante tenere a mente alcuni suggerimenti chiave:
- Verificare sempre se i dati soddisfano le assunzioni di ogni test prima di decidere quale utilizzare.
- Considerare l’utilizzo di approcci ibridi che combinano entrambi i tipi di test per aumentare la potenza e ridurre il tasso di errore di tipo I.
- Non fare affidamento esclusivamente sui valori p; considerare anche le dimensioni degli effetti e gli intervalli di confidenza nell’interpretazione dei risultati.
Essendo consapevoli di questi problemi e prendendo le precauzioni appropriate, è possibile fare un uso migliore dei metodi parametrici e non parametrici nella ricerca o nell’analisi.
Combinare test parametrici e non parametrici: vantaggi e svantaggi degli approcci ibridi
I metodi ibridi, noti anche come modelli misti o approcci combinati, stanno diventando sempre più popolari nell’analisi statistica. Questi approcci combinano elementi di entrambi i test parametrici e non parametrici per fornire analisi più robuste e flessibili. Il principale vantaggio dei metodi ibridi è che consentono di effettuare analisi integrate che possono tenere conto dei punti di forza e delle limitazioni di ciascun approccio.
Un esempio comune di metodo ibrido è l’uso di test non parametrici per convalidare o confermare i risultati ottenuti dai test parametrici. Ciò può essere particolarmente utile quando si lavora con campioni di piccole dimensioni o dati che non soddisfano le ipotesi di normalità o di varianze uguali richieste dai test parametrici. Un altro approccio consiste nell’utilizzare modelli misti che includono effetti fissi e casuali, consentendo analisi più sfumate che possono catturare relazioni complesse tra le variabili. In breve, i metodi ibridi offrono una gamma di opzioni per i ricercatori che vogliono sfruttare i vantaggi di entrambi gli approcci parametrici e non parametrici minimizzando i rispettivi svantaggi.
Vantaggi:
- Fornisce analisi più robuste e flessibili
- Consente analisi integrate
Svantaggi:
- Può essere complesso e richiedere tempo
- Richiede una attenta considerazione nella selezione dei metodi appropriati
Future Directions and Trends in Parametric and Nonparametric Tests: What to Expect
Guardando verso il futuro dell’analisi statistica, ci sono diversi sviluppi entusiasmanti all’orizzonte. Una zona che è pronta a fare un grande impatto è l’inferenza bayesiana, che consente di modellare in modo più flessibile e accurato insiemi di dati complessi. Incorporando la conoscenza precedente e aggiornando le credenze man mano che diventano disponibili nuovi dati, i metodi bayesiani possono fornire stime più robuste e previsioni migliori rispetto ai tradizionali approcci frequentisti.
Un’altra tendenza promettente nell’analisi statistica è l’uso crescente degli algoritmi di apprendimento automatico. Questi potenti strumenti possono gestire grandi quantità di dati e identificare schemi che potrebbero essere difficili o impossibili da rilevare con metodi tradizionali. Poiché l’apprendimento automatico continua a evolversi, è probabile che diventi una parte sempre più importante sia delle analisi parametriche che non parametriche.
Oltre a queste tecniche all’avanguardia, ci sono anche sforzi in corso per migliorare l’affidabilità e l’accuratezza dei metodi esistenti. Ad esempio, i ricercatori stanno sviluppando nuove procedure di stima robuste che possono produrre risultati accurati anche in presenza di valori anomali o altre fonti di rumore nei dati.
Infine, la modellizzazione multilivello è emersa come uno strumento prezioso per analizzare strutture di dati gerarchici come quelle presenti nella ricerca in scienze sociali o negli studi medici. Tenendo conto della variazione a più livelli (ad esempio, pazienti individuali all’interno degli ospedali), i modelli multilivello possono fornire intuizioni più sfumate su fenomeni complessi.
Per ribadire, è chiaro che ci sono molte direzioni entusiasmanti per la ricerca futura in statistica e campi correlati. Che tu stia lavorando con test parametrici o non parametrici – o una combinazione di entrambi – rimanere al passo con queste tendenze sarà essenziale per restare avanti in questo campo in rapida evoluzione.








