Haben Sie sich jemals in einem Meer von statistischem Fachjargon verloren gefühlt und Schwierigkeiten gehabt, zwischen parametrischen und nichtparametrischen Tests zu unterscheiden? Keine Sorge, mein Freund – Sie sind nicht allein. In der Welt der Datenanalyse und Forschungsmethodik ist das Verständnis der Unterschiede zwischen diesen beiden Arten von Tests entscheidend für eine genaue Interpretation und Berichterstattung der Ergebnisse.
Auf den ersten Blick mögen die Begriffe „parametrisch“ und „nichtparametrisch“ einschüchternd oder sogar einschüchternd wirken. Sie sind jedoch einfach unterschiedliche Ansätze zur Überprüfung von Hypothesen über Populationsparameter. Parametrische Tests gehen davon aus, dass die Daten einer bestimmten Verteilung folgen (in der Regel normal), während nichtparametrische Tests keine Annahmen über die Verteilung machen.
In diesem Artikel werden wir die Definitionen und Grundkonzepte beider Testarten sowie ihre Annahmen, Vorteile und Einschränkungen untersuchen. Wir werden auch praktische Beispiele und Überlegungen diskutieren, wann jeder Test verwendet werden sollte. Am Ende dieses Artikels werden Sie ein umfassendes Verständnis dieser Tests und ihrer Durchführung haben.
Wir werden uns tiefer mit Ein-Stichproben-, Zwei-Stichproben- und Gepaarten-Stichproben-Tests befassen und Schritt-für-Schritt-Anleitungen zur Durchführung von parametrischen und nichtparametrischen Tests mit Tipps für eine erfolgreiche Analyse bereitstellen. Anhand von Fallstudien und Beispielen werden reale Anwendungen untersucht.
Wir werden auch häufige Missverständnisse oder Fallstricke bei der Verwendung von parametrischen vs. nichtparametrischen Tests sowie hybride Ansätze, die beide Methoden kombinieren, behandeln.
Indem wir diese Themen zusammen in diesem Artikel untersuchen, hoffen wir, Forscher, Studenten und Fachleute in Statistik oder Datenanalyse mit Einblicken in zukünftige Richtungen für diese Ansätze zu befähigen, damit sie in ihren Feldern voraus bleiben können.
Parametrische und nichtparametrische Tests: Definitionen und Grundkonzepte
Parametrische und nichtparametrische Tests sind zwei Arten von statistischen Analysen, die verwendet werden, um Hypothesen über Populationseigenschaften zu testen. Der Hauptunterschied zwischen diesen Tests besteht darin, dass parametrische Tests bestimmte Annahmen über die zugrunde liegende Verteilung der Daten erfordern, während nichtparametrische Tests dies nicht tun.
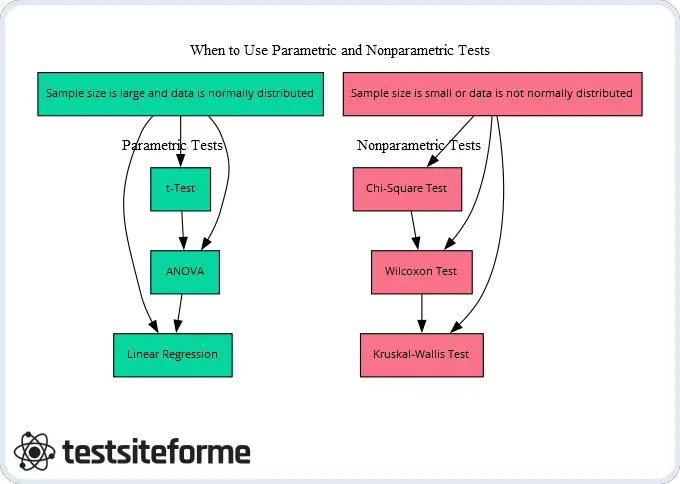
- Parametrische Tests: Dazu gehören t-Tests, ANOVA und Korrelationskoeffizienten-Analysen. Sie gehen davon aus, dass die analysierten Daten einer bestimmten Verteilung (normalerweise normal) folgen und stützen sich auf die Schätzung von Parametern wie Mittelwerten und Varianzen, um Rückschlüsse auf Populationseigenschaften zu ziehen. Parametrische Tests sind im Allgemeinen leistungsfähiger als nichtparametrische Tests, wenn die Annahmen erfüllt sind, können jedoch weniger robust sein, wenn diese Annahmen verletzt werden.
- Nichtparametrische Tests: Dazu gehören der Wilcoxon-Rangsummentest, der Kruskal-Wallis-Test und die Korrelationskoeffizienten-Analyse nach Spearman. Sie machen weniger Annahmen über die Verteilung der analysierten Daten und verwenden Methoden, die keine Parameterabschätzung oder Hypothesentests auf der Grundlage von Verteilungseigenschaften erfordern.
Es ist wichtig, jede Art von Test zu verstehen, da die Wahl eines Tests gegenüber einem anderen erhebliche Auswirkungen auf Ihre Forschungsergebnisse haben kann.
Bei der Durchführung von räumlichen Analysen oder der Messung von Wachstumsraten in Populationen kann es schwierig sein festzustellen, ob Ihre Daten einer Normalverteilung oder einer anderen spezifischen Verteilung entsprechen, die für parametrische Tests erforderlich ist. In solchen Fällen könnte Nicht-Parametrik eine bessere Wahl sein, da sie keine strengen Anforderungen an die Eingangsvariablen haben.
Das Fazit ist, dass das Verständnis grundlegender Konzepte wie Hypothesentests unerlässlich ist, bevor man sich für eine Methode entscheidet, da beide Vor- und Nachteile haben, je nachdem, was man mit dem Studiendesign erreichen möchte!
Annahmen parametrischer und nichtparametrischer Tests: Was Sie wissen müssen
Bevor Sie einen statistischen Test durchführen, ist es wichtig, die Annahmen zu verstehen, die parametrischen und nichtparametrischen Tests zugrunde liegen. Diese Annahmen sind entscheidend, da sie die Gültigkeit und Zuverlässigkeit Ihrer Ergebnisse beeinflussen. Die Hauptannahmen parametrischer Tests umfassen Homogenität der Varianz, Normalverteilung, Unabhängigkeit der Beobachtungen und gleiche Stichprobengröße. Nichtparametrische Tests hingegen machen viele dieser Annahmen nicht.
Homogenität der Varianz geht davon aus, dass die Variabilität der Datenpunkte in verschiedenen Gruppen oder Stichproben ähnlich ist. Diese Annahme ist für einige parametrische Tests wie t-Tests und ANOVA notwendig, da sie auf einem gemeinsamen Maß für die Varianz über Gruppen für eine genaue Interpretation beruhen. Normalverteilung bezieht sich auf die Annahme, dass die Daten einer glockenförmigen Kurve folgen, die als Normalverteilung bezeichnet wird. Dies ist auch für einige parametrische Tests notwendig, da sie davon ausgehen, dass die Daten eine Standardabweichung und einen Mittelwert haben.
Unabhängigkeit der Beobachtungen geht davon aus, dass jede Messung oder Beobachtung in einer Gruppe nicht von einer anderen Messung in einer anderen Gruppe oder einer Gruppe von Messungen innerhalb ihrer eigenen Gruppe abhängt. Dies bedeutet, dass es keine Korrelation zwischen Messungen geben sollte, die von verschiedenen Individuen oder Stichproben innerhalb jeder Gruppe genommen wurden.
Gleiche Stichprobengröße geht davon aus, dass alle verglichenen Gruppen eine gleiche Anzahl von Beobachtungen haben, um eine Verzerrung zugunsten einer bestimmten Gruppe während der Analyse zu vermeiden.
Es ist erwähnenswert, dass nichtparametrische Methoden nicht unbedingt dieselben Annahmen erfordern; stattdessen verlassen sie sich auf weniger strenge Annahmen wie Rangordnung anstelle von spezifischen Verteilungen oder Varianzen in ihren Eingabedatensätzen. Daher kann das Verständnis dieser Annahmen Ihnen helfen, basierend auf Ihrem Forschungsdesign zu entscheiden, welche Art von Test zu verwenden ist, während Sie falsche Interpretationen aufgrund verletzter zugrunde liegender Prinzipien vermeiden.
Annahmen parametrischer und nichtparametrischer Tests
Diese Tabelle vergleicht die Annahmen parametrischer und nichtparametrischer Tests und hebt Unterschiede im Typ der Daten hervor, die sie verarbeiten können, sowie Annahmen über Normalverteilung und Varianz.
| Annahme | Parametrischer Test | Nichtparametrischer Test |
|---|---|---|
| Art der Daten | Kontinuierlich, normal verteilt | Jeder Datentyp |
| Normalverteilung | Geht von normaler Verteilung der Daten aus | Geht nicht von normaler Verteilung der Daten aus |
| Varianz | Geht von gleicher Varianz über Gruppen aus | Geht nicht von gleicher Varianz über Gruppen aus |
Vorteile und Einschränkungen von parametrischen und nichtparametrischen Tests: Welchen sollten Sie wählen?
Bei der Wahl zwischen parametrischen und nichtparametrischen Tests gibt es mehrere Faktoren zu berücksichtigen. Die Vorteile von parametrischen Tests liegen in ihrer statistischen Power – sie sind tendenziell empfindlicher und genauer bei der Prüfung von Hypothesen über Mittelwerte und Varianzen, vorausgesetzt, bestimmte Bedingungen sind erfüllt. Wenn Sie beispielsweise normal verteilte Daten mit gleichen Varianzen über Gruppen haben, wird ein t-Test oder eine ANOVA wahrscheinlich präzisere Ergebnisse liefern als ein nichtparametrisches Äquivalent wie der Wilcoxon-Rangsummentest oder der Kruskal-Wallis-Test. Ein weiterer Vorteil von parametrischen Tests ist, dass sie in der Regel kleinere Stichprobengrößen als nichtparametrische Tests benötigen, um das gleiche Signifikanzniveau zu erreichen.
Auf der anderen Seite stammen die Einschränkungen von parametrischen Tests aus ihren Annahmen über die Datenverteilung, die in der Praxis nicht immer zutreffen können. Wenn Ihre Daten beispielsweise schief sind oder Ausreißer aufweisen, kann die Verwendung eines parametrischen Tests aufgrund von Verletzungen der Normalitäts- oder Homoskedastizitätsannahmen zu falschen Schlussfolgerungen führen. Nichtparametrische Tests sind im Allgemeinen robuster gegenüber solchen Abweichungen von idealen Bedingungen, da sie nicht auf spezifischen Wahrscheinlichkeitsverteilungen beruhen.
Welchen sollten Sie also wählen? Die Antwort hängt von Ihrer Forschungsfrage, dem Studiendesign und den verfügbaren Ressourcen ab. Hier ist eine Zusammenfassung einiger wichtiger Überlegungen:
Verwenden Sie parametrische Tests, wenn:
- Ihre Daten einer Normalverteilung folgen
- Sie gleiche Varianzen über Gruppen haben
- Sie eine höhere statistische Power wünschen
- Sie eine begrenzte Stichprobengröße haben
Verwenden Sie nichtparametrische Tests, wenn:
- Ihre Daten keiner Normalverteilung folgen
- Sie ungleiche Varianzen über Gruppen haben
- Sie eine größere Robustheit gegenüber Ausreißern oder anderen Anomalien wünschen
- Ihre Stichprobengröße groß genug ist
Denken Sie daran, dass diese Richtlinien keine absoluten Regeln sind – es kann Situationen geben, in denen hybride Ansätze oder alternative Methoden (z.B. Bootstrapping) besser für Ihre Bedürfnisse geeignet sind. Letztendlich geht es darum, die am besten geeignete Methode für Ihre spezifische Forschungsfrage zu wählen und sich dabei der Stärken und Schwächen in Bezug auf die Datenmerkmale und analytischen Ziele bewusst zu sein.
Wann man parametrische und nichtparametrische Tests verwenden sollte: Praktische Beispiele und Überlegungen
Wenn es darum geht, zwischen parametrischen und nichtparametrischen Tests zu wählen, gibt es mehrere praktische Beispiele und Überlegungen, die man im Auge behalten sollte. Ein wichtiger Faktor ist, ob Ihre Daten den Annahmen eines parametrischen Tests entsprechen. Diese Annahmen umfassen eine normale Verteilung, gleiche Varianzen und Unabhängigkeit der Beobachtungen. Wenn Ihre Daten eine dieser Annahmen verletzen, ist ein nichtparametrischer Test möglicherweise angemessener.
Eine weitere Überlegung ist die Art der Analyse, die Sie durchführen müssen. Wenn Sie beispielsweise daran interessiert sind, die Beziehung zwischen zwei kontinuierlichen Variablen zu bewerten, könnten Sie lineare Regression oder Korrelationskoeffizientenanalyse verwenden – beides sind parametrische Tests. Wenn Sie jedoch kategoriale oder ordinale Daten haben, die nicht in Intervallskalenmessungen umgewandelt werden können (z.B. Likert-Skalen), könnten nichtparametrische Tests wie Chi-Quadrat oder Mann-Whitney U nützlicher sein.
Hier sind einige weitere praktische Beispiele und Überlegungen für die Verwendung von parametrischen und nichtparametrischen Tests:
- ANOVA-Analyse: Wenn Sie Mittelwerte über drei oder mehr Gruppen vergleichen möchten (z.B. unterschiedliche Behandlungsbedingungen), ist ANOVA ein häufig verwendeter parametrischer Test, der eine normale Verteilung der Residuen annimmt.
- Gepaarter Stichproben-t-Test: Dies ist ein nützlicher parametrischer Test, wenn man zwei verwandte Stichproben vergleicht (z.B. Vor- vs. Nachtestergebnisse) mit normal verteilten Unterschieden.
- Wilcoxon-Test für gepaarte Stichproben: Eine nichtparametrische Alternative zum gepaarten Stichproben-t-Test, die verwendet wird, wenn die Annahme der Normalverteilung nicht erfüllt ist.
- Kruskal-Wallis H-Test: Dieser nichtparametrische Test kann als Alternative für ANOVA verwendet werden, wenn die Residuen der experimentellen Bedingungen nicht normal verteilt sind.
Kurz gesagt erfordert das Verständnis, wann man jeden Typ von Test verwenden sollte, sorgfältige Überlegungen basierend auf Ihrer Forschungsfrage und den Datenmerkmalen. Durch die Auswahl der richtigen Art von statistischer Methode für Ihre spezifischen Bedürfnisse erhöhen Sie Ihre Chancen, genaue Ergebnisse zu erzielen, die Ihre Ergebnisse angemessen widerspiegeln.
Verständnis der Unterschiede zwischen Ein-Stichproben-, Zwei-Stichproben- und Gepaarten-Stichproben-Tests
Wenn es um statistische Analysen geht, ist eine der wichtigsten Unterscheidungen zwischen parametrischen und nichtparametrischen Tests die Art der Daten, für die sie konzipiert sind. Insbesondere gibt es drei Haupttypen von Stichproben, mit denen Forscher typischerweise konfrontiert werden: Ein-Stichproben-, Zwei-Stichproben- und Gepaarte-Stichproben. Jeder von ihnen stellt einzigartige Herausforderungen für die Analyse von unabhängigen Daten, den Vergleich von gepaarten Stichproben, die Hypothesenprüfung mit einer einzigen Stichprobe und die unabhängige Beurteilung von Populationen dar.
Ein-Stichproben-Tests beinhalten den Vergleich eines Stichprobenmittelwerts oder einer Stichprobenproportion mit einem bekannten Standard- oder Populationswert. Zum Beispiel, nehmen wir an, Sie möchten testen, ob die durchschnittliche Größe der Schüler in Ihrer Schule signifikant von der nationalen Durchschnittsgröße abweicht. In diesem Fall würden Sie einen Ein-Stichproben-t-Test oder z-Test verwenden, abhängig davon, ob Sie die Standardabweichung der Größen in Ihrer Schülerpopulation kennen.
Zwei-Stichproben-Tests vergleichen Mittelwerte oder Proportionen von zwei unabhängigen Gruppen, die in keiner Weise miteinander verbunden sind. Wenn Sie beispielsweise die Wirksamkeit von zwei verschiedenen Behandlungen bei Patienten mit einer bestimmten Erkrankung im Laufe der Zeit vergleichen möchten (z.B. Messungen vor und nach der Behandlung), müssen Sie einen unabhängigen t-Test oder z-Test auf der Grundlage ihrer jeweiligen Mittelwerte und Varianzen durchführen.
Gepaarte-Stichproben-Tests beinhalten den Vergleich von Beobachtungen aus zwei abhängigen Gruppen, die aufgrund eines Kriteriums wie Alter, Geschlecht oder Behandlungszuweisung abgeglichen wurden. Diese Art des Vergleichs ermöglicht präzisere Ergebnisse durch Reduzierung der Variabilität aufgrund individueller Unterschiede zwischen den Probanden. Gemeinsame Beispiele sind Vor- vs. Nach-Interventionsmessungen innerhalb von Individuen (z.B. Blutdruckmessung vor und nach Einnahme von Medikamenten) sowie Geschwisterpaare, die nur durch die Geburtsreihenfolge unterschieden werden (d.h. Erstgeborene vs. Zweitgeborene). Zur statistischen Analyse solcher Datensätze sind spezialisierte Techniken wie gepaarte t-Tests erforderlich, die für korrelierte Fehler über Zeitpunkte innerhalb jedes individuellen Beobachtungspaars berücksichtigen.
Alles in allem kann das Verständnis, wann und wie man Ein-, Zwei- und Gepaarte-Stichproben-Tests anwendet, den Unterschied bei der Durchführung genauer statistischer Analysen mit realen Anwendungen in vielen Bereichen wie Medizin, Wirtschaft, Recht, Sozialwissenschaften, Ingenieurwesen und anderen ausmachen.
Eigenschaften und angemessene Verwendung von Ein-Stichproben-, Zwei-Stichproben- und Gepaarten-Stichproben-Tests
Diese Tabelle fasst die Unterschiede zwischen Ein-Stichproben-, Zwei-Stichproben- und Gepaarten-Stichproben-Tests zusammen und gibt Hinweise darauf, wann jeder Testtyp verwendet werden sollte.
| Testtyp | Vergleich | Annahmen | Angemessene Verwendung |
|---|---|---|---|
| Ein-Stichprobe | Stichprobenmittelwert vs. hypothetischer Wert | Normalität und Homogenität der Varianz | Testen, ob ein Stichprobenmittelwert signifikant von einem bekannten Wert abweicht |
| Zwei-Stichproben | Stichprobenmittelwerte von zwei unabhängigen Gruppen | Normalität und Homogenität der Varianz | Testen, ob die Mittelwerte von zwei unabhängigen Gruppen signifikant voneinander abweichen |
| Gepaarte Stichproben | Stichprobenmittelwerte von zwei verwandten Gruppen | Normalität und Homogenität der Varianz der Unterschiede | Testen, ob die Mittelwerte von zwei verwandten Gruppen (z.B. Vor- und Nachbehandlung) signifikant voneinander abweichen |
Wie man parametrische und nichtparametrische Tests durchführt: Schritt-für-Schritt-Anleitung und Tipps
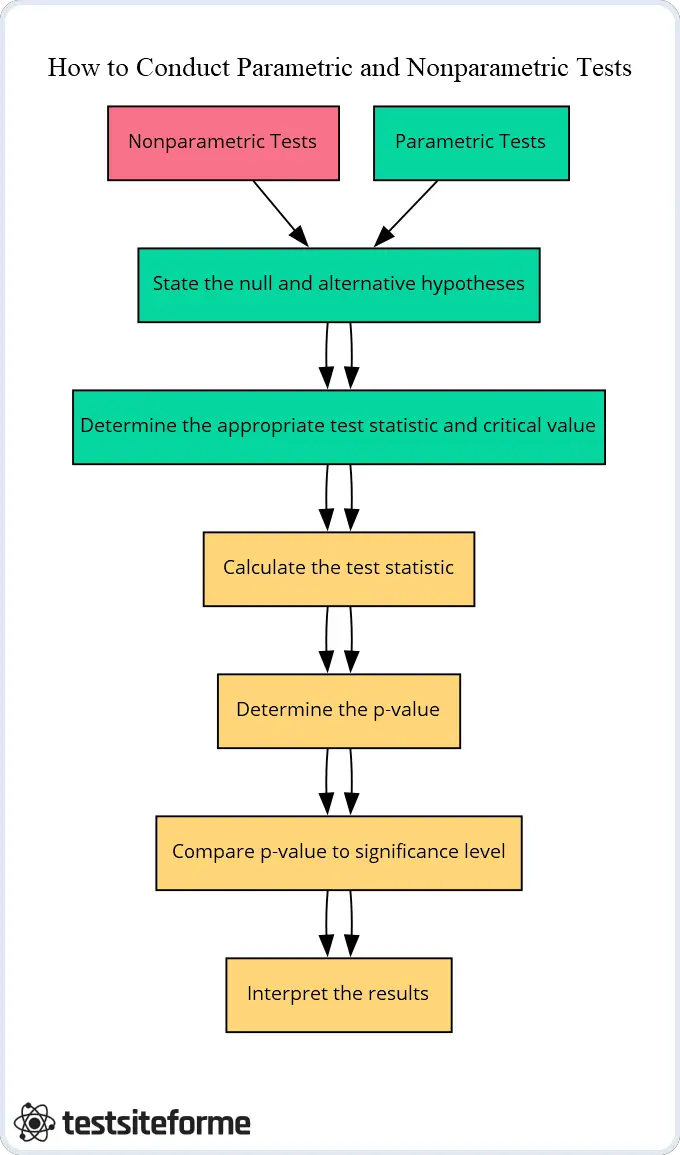
Wenn es darum geht, parametrische und nichtparametrische Tests durchzuführen, gibt es einige wichtige Schritte, die Sie befolgen müssen. Zunächst sollten Sie bestimmen, welche Art von Test für Ihre Datenanalysebedürfnisse geeignet ist. Dies hängt von mehreren Faktoren ab, einschließlich der Verteilung Ihrer Daten, dem Messniveau Ihrer Variablen und den Annahmen, die jedem Test zugrunde liegen.
Als nächstes müssen Sie Hypothese-Testverfahren einrichten, die es Ihnen ermöglichen, zu bewerten, ob es statistische Signifikanz in Ihren Ergebnissen gibt oder nicht. Dies beinhaltet die Festlegung einer Nullhypothese (die davon ausgeht, dass kein signifikanter Effekt vorliegt) und einer Alternativhypothese (die davon ausgeht, dass ein signifikanter Effekt vorliegt).
Sobald diese Schritte abgeschlossen sind, ist es an der Zeit, den Test tatsächlich durchzuführen. Bei parametrischen Tests mit normalverteilten Daten geht dies in der Regel mit der Berechnung eines t-Werts oder F-Werts mit mathematischen Formeln auf Basis von Mittelwerten und Standardabweichungen einher. Nichtparametrische Tests können das Ranking von Beobachtungen oder die Verwendung anderer Methoden beinhalten, die nicht auf Annahmen über Normalität beruhen.
Um die Genauigkeit Ihrer Ergebnisse zu gewährleisten und mögliche Verzerrungen oder Fehler bei der Interpretation zu minimieren, ist es wichtig, etablierte Richtlinien für die Durchführung dieser Arten von Tests sorgfältig zu befolgen. Dazu kann das Überprüfen von Ausreißern oder ungewöhnlichen Werten in Ihren Daten, die Auswahl angemessener Stichprobengrößen auf Basis von Power-Berechnungen und die Gewährleistung, dass alle notwendigen Annahmen erfüllt sind, bevor Sie mit der Analyse fortfahren, gehören.
Um durch den Lärm zu kommen, kann das Verständnis, wie man parametrische vs. nichtparametrische Tests durchführt, ein wesentliches Werkzeug für Forscher sein, die zuverlässige Methoden zur Bewertung der statistischen Signifikanz ihrer Ergebnisse benötigen. Durch die Einhaltung bewährter Praktiken für die Datenanalyse und die Berücksichtigung wichtiger Überlegungen wie Verteilungseigenschaften und Messniveaus können Sie dazu beitragen, genaue Ergebnisse zu erzielen und dabei häufige Fallstricke zu vermeiden.
Tips:
- Wählen Sie den geeigneten Test auf der Grundlage zugrunde liegender Annahmen aus
- Richten Sie Hypothesentestverfahren ein
- Führen Sie den Test durch, indem Sie Werte berechnen
- Befolgen Sie etablierte Richtlinien
- Überprüfen Sie Ausreißer
- Wählen Sie angemessene Stichprobengrößen aus
Real-World-Anwendungen von parametrischen und nichtparametrischen Tests: Fallstudien und Beispiele
Die Anwendungen von parametrischen und nichtparametrischen Tests in der realen Welt sind vielfältig und umfangreich. Diese Tests können in verschiedenen Bereichen eingesetzt werden, wie zum Beispiel im Marketing, in der medizinischen Forschung, bei der Bildungsbewertung und bei der Umweltüberwachung. Schauen wir uns einige Beispiele genauer an.
Im Marketing können parametrische Tests dazu beitragen, die Wirksamkeit von Werbekampagnen zu messen, indem sie Click-Through-Raten oder Konversionsraten analysieren. Andererseits können nichtparametrische Tests nützlich sein, um Verbrauchervorlieben auf der Grundlage von Umfrageantworten oder Bewertungen zu identifizieren.
Die medizinische Forschung befasst sich oft mit der Untersuchung der Auswirkungen von Behandlungen oder Interventionen auf die Ergebnisse von Patienten. Parametrische Tests werden häufig verwendet, um Mittelwerte zwischen zwei Gruppen (z. B. Behandlungsgruppe versus Kontrollgruppe) zu vergleichen, wenn bestimmte Annahmen über Normalverteilung und gleiche Varianzen erfüllt sind. Nichtparametrische Alternativen wie der Wilcoxon-Rangsummentest können bevorzugt werden, wenn diese Annahmen nicht erfüllt sind oder die Daten stark verzerrt sind.
Die Bildungsbewertung ist ein weiterer Bereich, in dem parametrische und nichtparametrische Tests umfassend angewendet wurden. Zum Beispiel können t-Tests verwendet werden, um festzustellen, ob es einen signifikanten Unterschied in den Durchschnittswerten zwischen zwei Gruppen von Schülern gibt (z. B. diejenigen, die Nachhilfe erhalten haben, gegenüber denen, die es nicht getan haben). Alternativ können nichtparametrische Methoden wie der Mann-Whitney-U-Test auch Einblicke in Unterschiede zwischen Gruppen geben, die Normalitätsannahmen nicht erfüllen.
Die Umweltüberwachung umfasst Prozesse zur Messung physikalischer Parameter wie Temperatur oder Luftqualität im Laufe der Zeit an verschiedenen Standorten. In diesem Fall könnten parametrische Tests wie die ANOVA (Varianzanalyse) dazu beitragen, räumliche Trends zu erkennen, während die zeitliche Variation innerhalb jedes Standorts separat berücksichtigt wird. Nichtparametrische Tests wie der Kruskal-Wallis-Test könnten auch nützlich sein, wenn die Daten nicht den Anforderungen für ANOVA-Annahmen entsprechen.
Zusammenfassend lässt sich sagen, dass das Verständnis der Verwendung von sowohl parametrischen als auch nichtparametrischen Tests Ihre Fähigkeit verbessern wird, aussagekräftige Schlussfolgerungen aus Ihren Datenanalysenergebnissen zu ziehen, unabhängig davon, ob Sie Click-Through-Raten für eine Werbekampagne analysieren oder die Auswirkungen eines neuen Medikaments auf die Ergebnisse von Patienten untersuchen!
Bevor Sie sich entscheiden, ob Sie einen parametrischen oder nichtparametrischen Test in Ihrer Forschung verwenden möchten, sollten Sie die Natur Ihrer Daten und die Annahmen, die jedem Testtyp zugrunde liegen, berücksichtigen. Machen Sie keine Annahmen aufgrund von Bequemlichkeit oder Vertrautheit; wählen Sie stattdessen den geeigneten Test für Ihre spezifische Forschungsfrage und seien Sie bereit, Ihre Wahl mit fundierter Argumentation und Evidenz zu verteidigen. Denken Sie daran, dass die Wahl der richtigen statistischen Tests den Unterschied zwischen genauen Schlussfolgerungen und irreführenden Ergebnissen bedeuten kann.
Gängige Missverständnisse und Fallstricke bei der Verwendung von parametrischen und nicht-parametrischen Tests
Es ist leicht, in gängige Missverständnisse und Fallstricke zu geraten, wenn man parametrische und nicht-parametrische Tests verwendet. Einer der häufigsten Fehler besteht darin anzunehmen, dass parametrische Tests immer eine Normalverteilungsannahme für die Datenverteilung erfordern. Während viele parametrische Tests eine Normalverteilung voraussetzen, gibt es Ausnahmen wie t-Tests mit kleinen Stichproben, die Abweichungen von der Normalverteilung bis zu einem gewissen Grad tolerieren können.
Ein weiteres Missverständnis besteht darin anzunehmen, dass nicht-parametrische Tests immer robuster sind als parametrische Tests. Während es wahr ist, dass nicht-parametrische Tests in der Regel keine Annahmen über gleiche Varianzen oder zugrunde liegende Verteilungen erfordern, können sie dennoch in bestimmten Szenarien Einschränkungen haben. Zum Beispiel können nicht-parametrische Tests weniger leistungsfähig sein als ihre parametrischen Pendants bei der Erkennung von Unterschieden zwischen Gruppen, insbesondere wenn die Stichprobengröße klein ist oder wenn es Bindungen in den Daten gibt.
Um diese Missverständnisse und Fallstricke zu vermeiden, ist es wichtig, sich an einige wichtige Tipps zu halten:
- Überprüfen Sie immer, ob Ihre Daten den Annahmen jedes Tests entsprechen, bevor Sie sich für einen entscheiden.
- Erwägen Sie die Verwendung hybrider Ansätze, die beide Arten von Tests kombinieren, um die Leistung zu erhöhen und die Fehlerart I zu reduzieren.
- Verlassen Sie sich nicht ausschließlich auf p-Werte; berücksichtigen Sie auch Effektgrößen und Konfidenzintervalle bei der Interpretation von Ergebnissen.
Indem Sie sich dieser Probleme bewusst sind und angemessene Vorsichtsmaßnahmen ergreifen, können Sie sowohl parametrische als auch nicht-parametrische Methoden in Ihrer Forschung oder Analyse besser nutzen.
Kombination von parametrischen und nichtparametrischen Tests: Vor- und Nachteile hybrider Ansätze
Hybride Methoden, auch bekannt als gemischte Modelle oder kombinierte Ansätze, werden in der statistischen Analyse immer beliebter. Diese Ansätze kombinieren Elemente von parametrischen und nichtparametrischen Tests, um robustere und flexiblere Analysen zu ermöglichen. Der Hauptvorteil hybrider Methoden besteht darin, dass sie integrierte Analysen ermöglichen, die sowohl die Stärken als auch die Grenzen jedes Ansatzes berücksichtigen können.
Ein häufiges Beispiel für einen hybriden Ansatz ist die Verwendung von nichtparametrischen Tests zur Validierung oder Bestätigung der Ergebnisse, die aus parametrischen Tests gewonnen wurden. Dies kann besonders nützlich sein, wenn man es mit kleinen Stichproben oder Daten zu tun hat, die nicht den Annahmen der Normalverteilung oder der gleichen Varianzen entsprechen, die von parametrischen Tests benötigt werden. Ein anderer Ansatz besteht darin, gemischte Modelle zu verwenden, die sowohl feste als auch zufällige Effekte enthalten und damit nuanciertere Analysen ermöglichen, die komplexe Beziehungen zwischen Variablen erfassen können. Kurz gesagt bieten hybride Methoden eine Vielzahl von Optionen für Forscher, die die Vorteile sowohl von parametrischen als auch von nichtparametrischen Ansätzen nutzen möchten, während sie die jeweiligen Nachteile minimieren.
Vorteile:
- Bietet robustere und flexiblere Analysen
- Ermöglicht integrierte Analysen
Nachteile:
- Kann komplex und zeitaufwendig sein
- Erfordert sorgfältige Überlegungen bei der Auswahl geeigneter Methoden
Zukünftige Entwicklungen und Trends in parametrischen und nichtparametrischen Tests: Was zu erwarten ist
Wenn wir in die Zukunft der statistischen Analyse schauen, gibt es mehrere aufregende Entwicklungen am Horizont. Ein Bereich, der dazu beitragen wird, ist die bayesianische Inferenz, die eine flexiblere und genauere Modellierung komplexer Datensätze ermöglicht. Durch die Einbeziehung von Vorwissen und die Aktualisierung von Überzeugungen, wenn neue Daten verfügbar werden, können bayesianische Methoden robustere Schätzungen und bessere Vorhersagen als traditionelle frequentistische Ansätze liefern.
Ein weiterer vielversprechender Trend in der statistischen Analyse ist der wachsende Einsatz von Machine-Learning-Algorithmen. Diese leistungsstarken Werkzeuge können große Datenmengen verarbeiten und Muster identifizieren, die mit traditionellen Methoden schwer oder unmöglich zu erkennen wären. Da Machine Learning weiterentwickelt wird, ist es wahrscheinlich, dass es ein zunehmend wichtiger Bestandteil sowohl parametrischer als auch nichtparametrischer Analysen wird.
Neben diesen innovativen Techniken gibt es auch laufende Bemühungen, die Zuverlässigkeit und Genauigkeit bestehender Methoden zu verbessern. Zum Beispiel entwickeln Forscher neue robuste Schätzverfahren, die auch bei Ausreißern oder anderen Quellen von Rauschen in den Daten genaue Ergebnisse liefern können.
Schließlich hat sich die Mehrebenenmodellierung als wertvolles Werkzeug zur Analyse hierarchischer Datenstrukturen wie sie in der Sozialforschung oder medizinischen Studien vorkommen, herausgestellt. Durch die Berücksichtigung von Variationen auf mehreren Ebenen (z.B. individuelle Patienten innerhalb von Krankenhäusern) können Mehrebenenmodelle nuanciertere Einblicke in komplexe Phänomene bieten.
Zusammenfassend lässt sich sagen, dass es viele aufregende Richtungen für zukünftige Forschung in Statistik und verwandten Bereichen gibt. Ob Sie mit parametrischen oder nichtparametrischen Tests arbeiten – oder einer Kombination aus beiden – auf dem neuesten Stand dieser Trends zu bleiben, wird entscheidend sein, um in diesem schnelllebigen Bereich voraus zu bleiben.








