Una prueba ANOVA (análisis de la varianza) es un tipo de prueba estadística que se utiliza para determinar si existe una diferencia estadísticamente significativa entre dos o más grupos categóricos mediante la comprobación de las diferencias de las medias utilizando la varianza. Fue desarrollada por Ronald Fisher en 1918.
Otra parte clave del ANOVA es que divide la variable independiente en 2 o más grupos. Por ejemplo, se puede esperar que uno o más grupos influyan en la variable dependiente, mientras que el otro grupo se utiliza como grupo de control y no se espera que influya en la variable dependiente.
Supuestos del ANOVA
Los supuestos de la prueba ANOVA son los mismos que los supuestos generales de cualquier prueba paramétrica:
- Un ANOVA sólo puede llevarse a cabo si no existe ninguna relación entre los sujetos de cada muestra. Esto significa que los sujetos del primer grupo no pueden estar también en el segundo grupo (por ejemplo, muestras independientes/entre grupos).
- Los diferentes grupos/niveles deben tener tamaños de muestra iguales.
- Un ANOVA sólo puede llevarse a cabo si la variable dependiente tiene una distribución normal, de modo que las puntuaciones medias sean las más frecuentes y las puntuaciones extremas las menos frecuentes.
- Las varianzas de la población deben ser iguales (es decir, homoscedásticas). Homogeneidad de la varianza significa que la desviación de las puntuaciones (medida por el rango o la desviación estándar, por ejemplo) es similar entre las poblaciones.
Tipos de pruebas ANOVA
Existen diferentes tipos de pruebas ANOVA. Los dos más comunes son el de «una vía» y el de «dos vías».
La diferencia entre estos dos tipos depende del número de variables independientes en su prueba.
ANOVA de una vía
Un ANOVA (análisis de la varianza) de una vía tiene una variable independiente categórica (también conocida como factor) y una variable dependiente continua (es decir, de nivel de intervalo o proporción) normalmente distribuida.
La variable independiente divide los casos en dos o más niveles, categorías o grupos mutuamente excluyentes.
La prueba ANOVA de una vía para las diferencias en las medias de la variable dependiente se desglosa por los niveles de la variable independiente.
Un ejemplo de análisis unidireccional incluye la prueba de una intervención terapéutica (TCC, medicación, placebo) sobre la incidencia de la depresión en una muestra clínica.
Nota: Tanto el ANOVA unidireccional como la prueba t de muestras independientes pueden comparar las medias de dos grupos. Sin embargo, sólo el ANOVA de una vía puede comparar las medias de tres o más grupos.
ANOVA de dos vías (factorial)
Un ANOVA (análisis de la varianza) de dos vías tiene dos o más variables independientes categóricas (también conocidas como factor), y una variable dependiente continua (es decir, de nivel de intervalo o proporción) normalmente distribuida.
Las variables independientes dividen los casos en dos o más niveles, categorías o grupos mutuamente excluyentes. Un ANOVA de dos vías también se denomina ANOVA factorial.
Un ejemplo de ANOVA factorial incluye la comprobación de los efectos del contacto social (alto, medio, bajo), la situación laboral (empleado, autónomo, desempleado, jubilado) y los antecedentes familiares (sin antecedentes familiares, algunos antecedentes familiares) sobre la incidencia de la depresión en una población (la variable de respuesta).
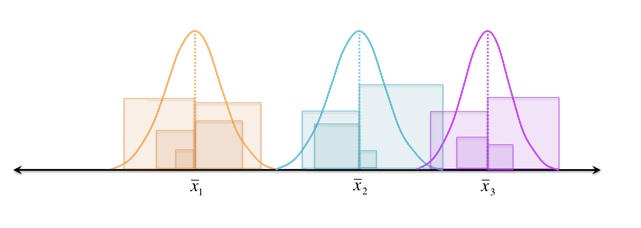
¿Qué son los «grupos» o «niveles»?
Los niveles son diferentes agrupaciones dentro de la misma variable independiente.
Por ejemplo, si la variable categórica independiente es «huevos», los niveles podrían ser «no orgánico», «orgánico» y «orgánico libre». La variable dependiente podría ser el precio por docena de huevos.
Comprender el valor F del ANOVA
La estadística de la prueba para un ANOVA se denomina F. La fórmula del ANOVA es F = varianza causada por el tratamiento/varianza debida al azar.
El valor F del ANOVA puede indicar si existe una diferencia significativa entre los niveles de la variable independiente, cuando p < 0,05. Así, un valor F más alto indica que las variables de tratamiento son significativas.
Tenga en cuenta que el ANOVA por sí solo no nos dice específicamente qué medias fueron diferentes entre sí. Para determinarlo, tendríamos que seguir con pruebas de comparaciones múltiples (o post-hoc).
Cuando la prueba F inicial indica que existen diferencias significativas entre las medias de los grupos, las pruebas post hoc son útiles para determinar qué medias específicas son significativamente diferentes cuando no se tienen hipótesis específicas que se deseen probar.
Las pruebas post hoc comparan cada par de medias (como las pruebas t), pero a diferencia de las pruebas t, corrigen la estimación de la significación para tener en cuenta las comparaciones múltiples.
¿Qué significa «réplica»?
La replicación requiere que un estudio se repita con diferentes sujetos y experimentadores. Esto permitiría a un analista estadístico confirmar un estudio anterior poniendo a prueba la misma hipótesis con una nueva muestra.
¿Cómo ejecutar un ANOVA?
Para grandes conjuntos de datos, es mejor ejecutar un ANOVA en un software estadístico como R o Stata. Refiriéndonos a nuestro ejemplo de los huevos anterior.
A los huevos no orgánicos, orgánicos y orgánicos en libertad se les asignarían valores cuantitativos (1,2,3) y servirían como nuestra variable de tratamiento independiente, mientras que el precio por docena de huevos serviría como variable dependiente. Otras variables erróneas pueden ser «Marca» o «Fecha de puesta».
Utilizando los datos y el comando aov() en R, podríamos entonces determinar el impacto que tiene el Tipo de Huevo en el precio por docena de huevos.
¿Cuál es la diferencia entre un ANOVA y una prueba t?
Las pruebas t y las pruebas ANOVA son técnicas estadísticas que se utilizan para comparar las diferencias de las medias y los márgenes de las distribuciones en las poblaciones.
La prueba t determina si dos poblaciones son estadísticamente diferentes entre sí, mientras que las pruebas ANOVA se utilizan cuando se quiere probar más de dos niveles dentro de una variable independiente.
Volviendo a nuestro ejemplo de los huevos, la prueba de los no orgánicos frente a los orgánicos requeriría una prueba t, mientras que la adición de los criados en libertad como tercera opción exige un ANOVA. En lugar de generar un estadístico t, el ANOVA da lugar a un estadístico f para determinar la significación estadística.
FAQ
¿Qué son los grados de libertad en el ANOVA de una y dos vías?
Los grados de libertad (DF) son el número de datos independientes. En el análisis ANOVA, una vez calculada la suma de cuadrados (por ejemplo, SStr, SSE), se divide por los DF correspondientes para obtener los cuadrados medios (por ejemplo, MStr, MSE), que son la varianza de la cantidad correspondiente.
¿Qué es el valor p en el ANOVA?
El valor P es la probabilidad de obtener un cociente F igual o mayor que el observado, suponiendo que la hipótesis nula de ausencia de diferencias entre las medias de los grupos sea cierta.
¿Cuál es la diferencia entre la prueba F y el ANOVA?
La prueba F se utiliza para determinar si las medias de dos o más poblaciones son estadísticamente diferentes entre sí. El ANOVA (análisis de la varianza) es una prueba más amplia que compara las medias con un grupo de control y con otros grupos experimentales, y también determina si existe una diferencia estadísticamente significativa entre las medias.
El ANOVA separa la varianza dentro del grupo de la varianza entre los grupos y la prueba F es la relación del error medio al cuadrado entre estos dos grupos.
El ANOVA es una herramienta de análisis estadístico común en el diseño experimental; la prueba F es más común en el análisis posterior al experimento.
¿Existe un tamaño mínimo de muestra para el ANOVA?
No hay un tamaño mínimo de muestra para el ANOVA, pero al mismo tiempo, podría tener problemas con la potencia estadística, que es su capacidad para rechazar una hipótesis nula falsa. Si las diferencias del tamaño del efecto entre la línea de base y las otras medidas no son lo suficientemente grandes, es posible que no pueda rechazar la hipótesis nula.
¿Cuáles son las limitaciones del ANOVA?
El ANOVA funciona mejor cuando hay una varianza igual entre los grupos y las poblaciones de las que se extraen los datos están distribuidas de forma aproximadamente normal.
La prueba de ANOVA también es relativamente robusta a las violaciones de los supuestos de la prueba. Sin embargo, no es tan robusta como la prueba T o las pruebas post-hoc (por ejemplo, Scheffe, Tukey, etc.). También hay que tener en cuenta que la prueba ANOVA no es capaz de detectar diferencias entre proporciones (por ejemplo, comparando la proporción de encuestados que están de acuerdo y en desacuerdo con una afirmación).
¿Qué es la hipótesis nula en el ANOVA?
La hipótesis nula en el ANOVA es la suposición de que no hay diferencia entre las medias de los grupos. La hipótesis nula se contrasta con la hipótesis alternativa, que es que hay una diferencia entre las medias de los grupos. Si los datos muestran que no hay diferencia entre las medias de los grupos, se apoya la hipótesis nula.
Te recomiendo que veas el siguiente vídeo, que hace un excelente trabajo para reforzar lo que ya has aprendido aquí:







